Hans Walser, [20240308]

Einmaleins

Anregung: Zvonimir Durcevic, Wien

1 Worum es geht

Spielerei mit symmetrischen Figuren in der Multiplikationstafel.

2 Multiplikationstafel

Die Abbildung 1 zeigt die Multiplikationstafel von 1 bis 12.

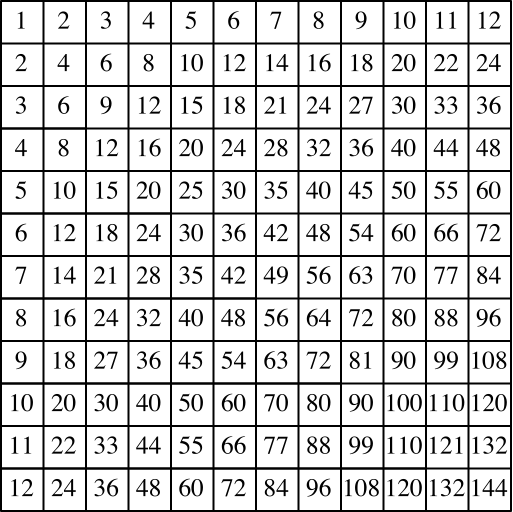
Abb. 1: Multiplikationstafel

3 Zwei Symmetrieachsen

Wir wählen ein beliebiges Startfeld und legen die Zeile und die Spalte durch das Startfeld als Symmetrieachse fest (Abb. 2).

Abb. 2: Startfeld und Symmetrieachsen

4 Symmetrische Figur

Nun zeichnen wir eine beliebige aus Feldquadraten zusammengesetzte Figur mit diesen Symmetrieachsen (Abb. 3).

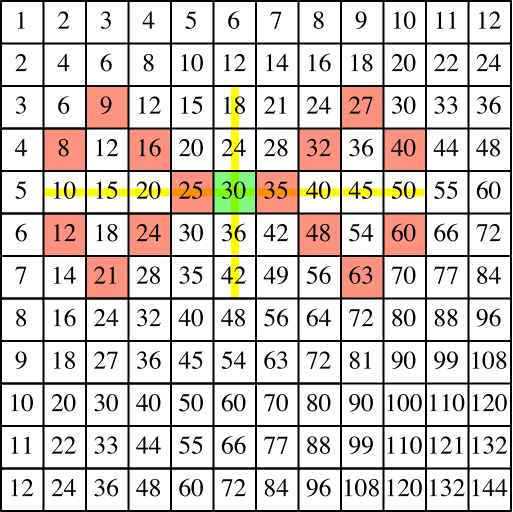
Abb. 3: Symmetrische Figur

5 Mittelwert

Jetzt zählen wir alle Zahlen in den Feldern der symmetrischen Figur zusammen:

Summe = 9 + 27 + 8 + 16 + 32 + 40 + 25 + 35 + 12 + 24 + 48 + 60 + 21 + 63 = 420

Für den Mittelwert (Durchschnitt, arithmetisches Mittel) dieser 14 Zahlen erhalten wir:

Mittelwert = 420/14 = 30

Dies ist genau die Zahl im Startfeld.

6 Allgemein

Für ein beliebiges Startfeld ergibt sich bei einer Figur mit Symmetrieachsen durch das Startfeld als Mittelwert der Zahlen in der symmetrischen Figur die Zahl im Startfeld.

7 Beweis

7.1 Zahlen auf einer Symmetrieachse

Die Zahlen in den Zeilen oder in den Spalten der Multiplikationstafel bilden je eine Folge mit konstantem Zuwachs (arithmetische Folge (erster Ordnung)).

Wir können zwei symmetrisch liegende Zahlen mit einer „Hantel“ zusammenfassen (Abb. 4). Die Mitte der Hantelstange ist das Startfeld, die zugehörige Zahl daher der Mittelwert der beiden Zahlen in den Gewichtskugeln der Hantel.

Abb. 4: Auf einer Symmetrieachse

7.2 Rechtecke

Zu einem Feld außerhalb der Symmetrieachsen gibt es aus Symmetriegründen drei weitere Felder, so dass die vier Felder die Ecken eines Rechteckes bilden (Abb. 5).

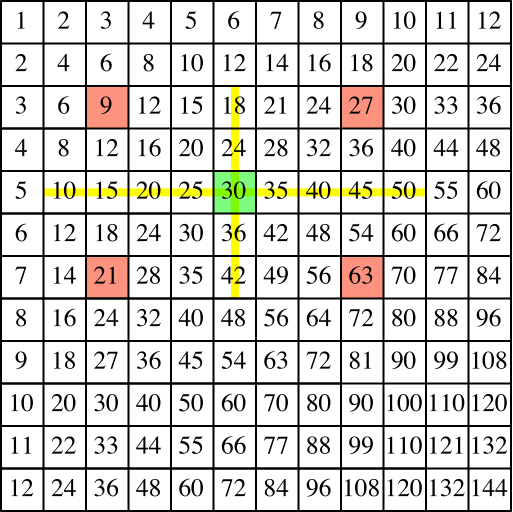
Abb. 5: Rechteck

Wir fassen je die beiden in derselben Zeile liegenden Ecken mit einer Hantel zusammen (Abb. 6). In der Mitte erscheint jeweils der Mittelwert der beiden Zahlen in den zugehörigen Ecken.

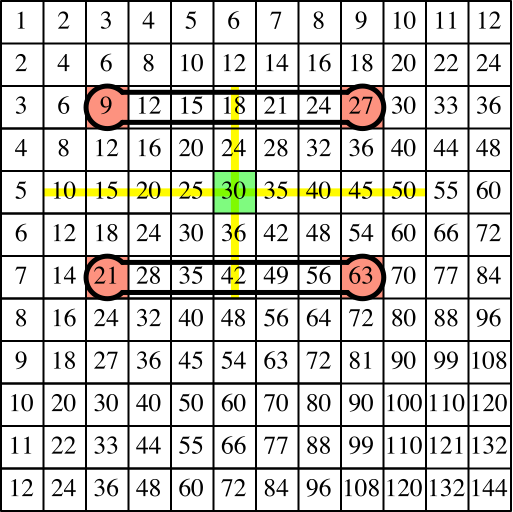
Abb. 6: Zwei Hanteln

Nun fassen wir die beiden Mittelwerte mit einer senkrechten Hantel zusammen (Abb. 7). Die Zahl im Startfeld ist somit der Mittelwert der vier Zahlen in den Ecken des Rechtecks.

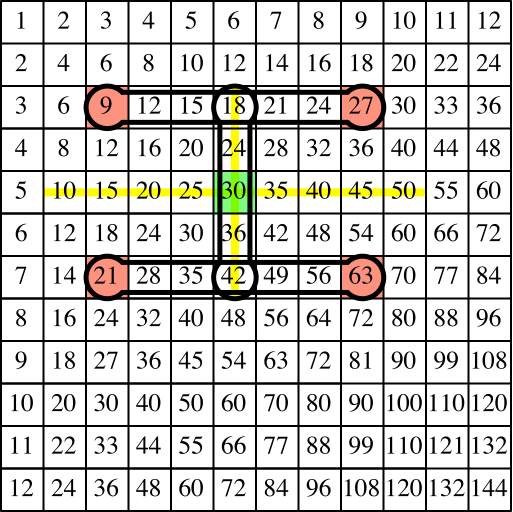
Abb. 7: Senkrechte Hantel

Natürlich geht es auch andersherum (Abb. 8 und 9).

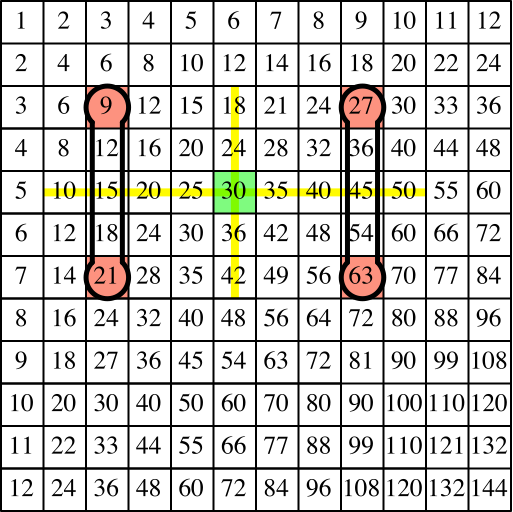
Abb. 8: Andersherum mit senkrechten Hanteln

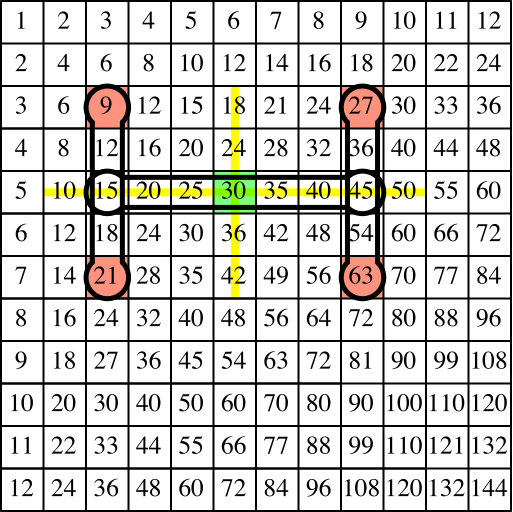
Abb. 9: Zusammenfassung mit waagerechter Hantel

7.3 Zusammensetzung

Unsere Figur mit den beiden Symmetrieachsen ist aus symmetrisch liegenden Zahlenpaaren in den Symmetrieachsen sowie Rechtecken zusammengesetzt. Daher gilt die Mittelwerteigenschaft für die Gesamtfigur.

8 Trapez

8.1 Spezielles Trapez

Wir passen ein gleichschenkliges Trapez so ein, dass seine Symmetrieachse und die Mittelparallele waagerecht und/oder senkrecht durch das Startfeld verlaufen (Abb. 10). Auch hier gilt die Mittelwerteigenschaft.

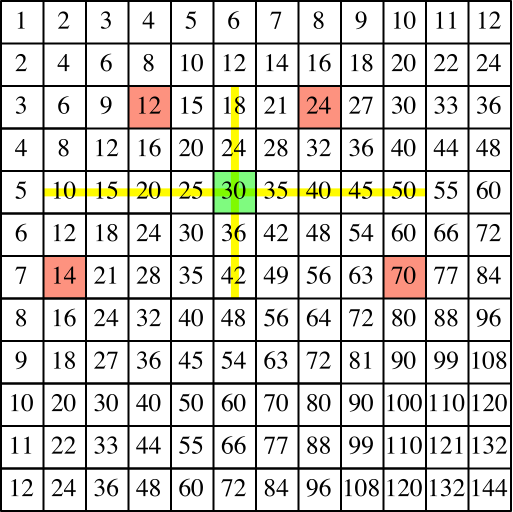
Abb. 10: Trapez

8.2 Beweis

Für den Beweis können wir mit Hanteln arbeiten. Wir beginnen mit Hanteln auf den beiden Parallelseiten (Abb. 11).

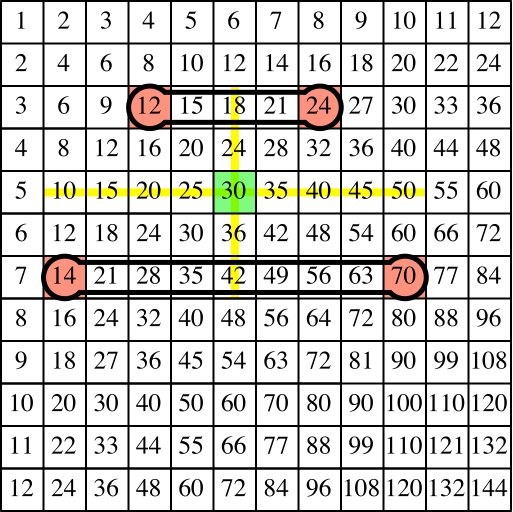
Abb. 11: Hanteln auf Parallelseiten

Anschließend fassen wir mit einer Hantel auf der Symmetrieachse zusammen (Abb. 12).

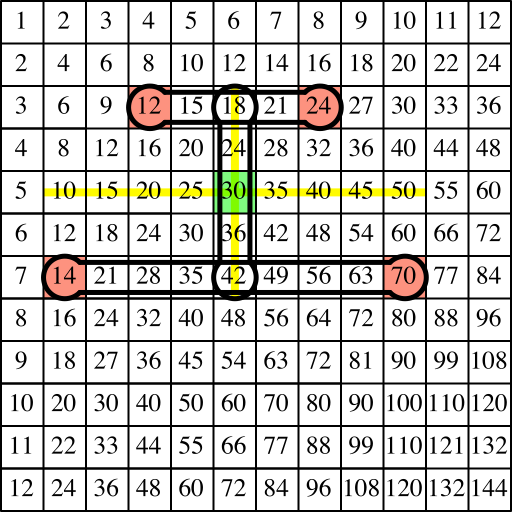
Abb. 12: Hantel auf Symmetrieachse

Damit ist die Mittelwerteigenschaft gezeigt.

8.3 Hanteln auf Schrägseiten?

Bei Hanteln auf den Schrägseiten (Abb. 13) erleben wir zunächst eine Enttäuschung. Es geht nicht. Die Mittelwerte stimmen nicht. Auf der linken Schrägseite müsste der Mittelwert 13 erscheinen, auf der rechten Schrägseite der Mittelwert 47. Was wir links zu viel haben, haben wir rechts zu wenig.

Das liegt daran, dass wir auf den Schrägen der Multiplikationstafel keine arithmetischen Folgen erster Ordnung haben, sondern solche zweiter Ordnung, also mit einem quadratischen Bildungsgesetz. Am augenfälligsten ist dies auf der Diagonalen von links oben nach rechts unten, wo die Quadratzahlen erscheinen.

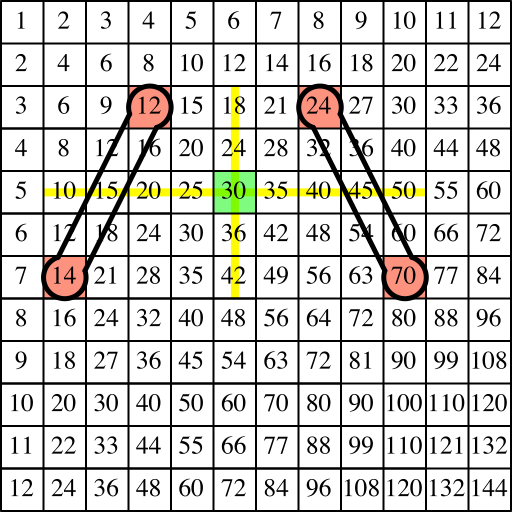
Abb. 13: Schrägseiten

Wir mogeln nun etwas und korrigieren die richtigen Mittelwerte hinein (Abb. 14).

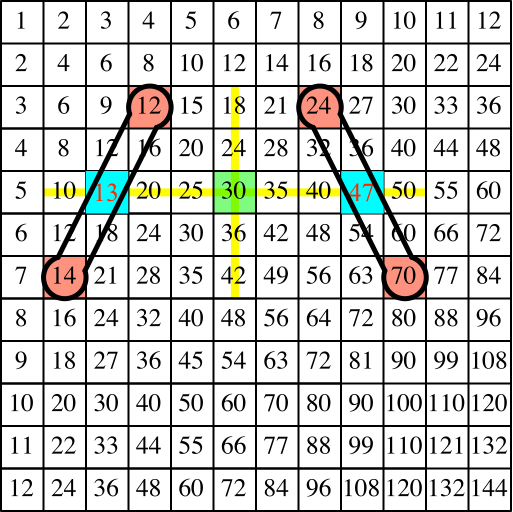
Abb. 14: Korrigierte Mittelwerte

Wenn wir jetzt mit einer Hantel auf der Mittellinie zusammenfassen, ergibt sich das gewünschte Resultat (Abb. 15). Ist unser Vorgehen korrekt?

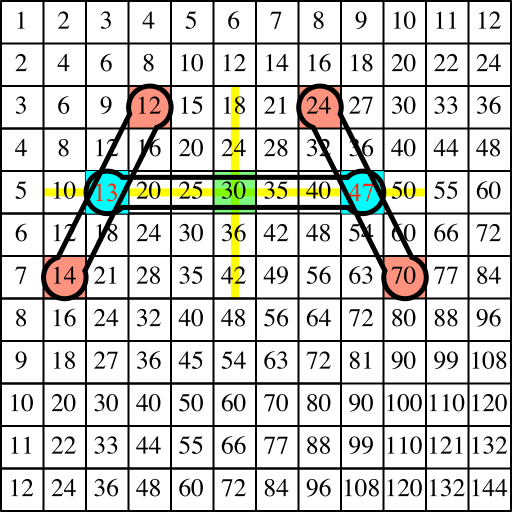
Abb. 15: Mittelwert

8.4 Kombinationen

Wir können nun kombinieren, zum Beispiel zwei Trapeze (Abb. 16).

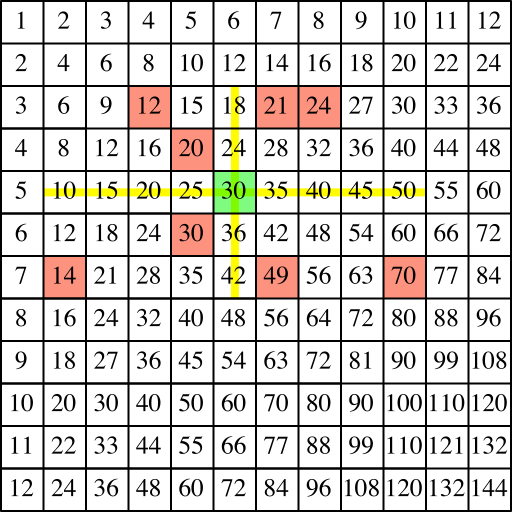
Abb. 16: Kombination

Weblinks

Hans Walser: Einmaleins

https://walser-h-m.ch/hans/Miniaturen/E/Einmaleins/Einmaleins.html

Hans Walser: Einmaleins

https://walser-h-m.ch/hans/Miniaturen/E/Einmaleins2/Einmaleins2.html