1 Worum es geht

Spielerei in der Multiplikationstabelle. Rösselsprung

2 Multiplikationstabelle

Die Abbildung 1 zeigt die Multiplikationstabelle von 1 bis 10

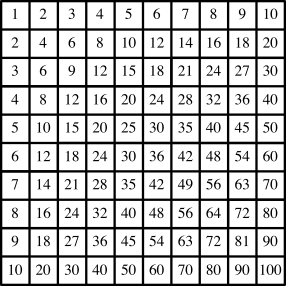
Abb. 1: Kleines Einmaleins

3 Rösselsprung

Wir beginnen in der ersten Spalte (am linken Rand) und arbeiten uns mit dem Rösselsprung (eins nach rechts, zwei nach oben) bis zum oberen Rand. Die Abbildung 2 zeigt das Beispiel mit der Startzahl 9.

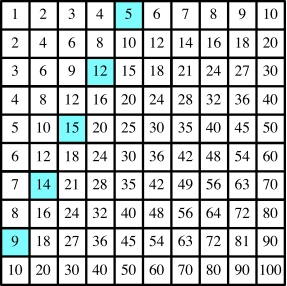
Abb. 2: Startzahl 9

Wir addieren die Zahlen auf diesem Weg (Abb. 3).

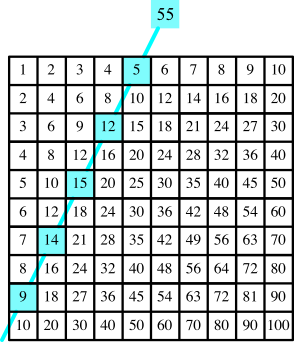
Abb. 3: Rösselsprung-Summe

Die Abbildung 4 zeigt das Entsprechende für die Startzahl 8.

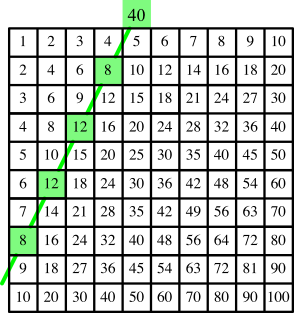
Abb. 4: Startzahl 8

Wir sehen, dass wir am oberen Rand ein unterschiedliches Verhalten haben. Die Rösselsprung-Wege der ungeraden Startzahlen und die Rösselsprung-Wege der geraden Startzahlen enden unterschiedlich am oberen Rand. Daher drängt sich eine Fallunterscheidung gerade/ungerade auf.

4 Ungerade Startzahlen

Die Abbildung 5 zeigt die Wege für die ungeraden Startzahlen, soweit sie im kleinen Einmaleins sichtbar sind. Natürlich können wir die Multiplikationstabelle beliebig nach unten und nach rechts verlängern und erhalten so weitere Rösselsprung-Wege.

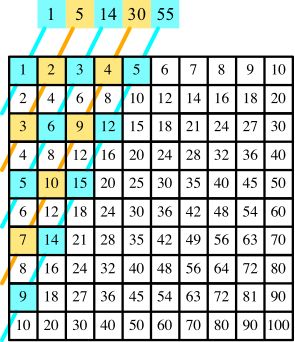
Abb. 5: Ungerade Startzahlen

Wir erhalten die Summenfolge 1, 5, 14, 30, 55, ... .

Diese Folge finden wir auch wie folgt: Wir dividieren im Pascal-Dreieck alle Einträge durch 4 (Abb. 6). In der dritten Schrägzeile (die Nummerierung beginnt links mit der nullten Schrägzeile) ist jede zweite Zahl ein Element unserer Folge.

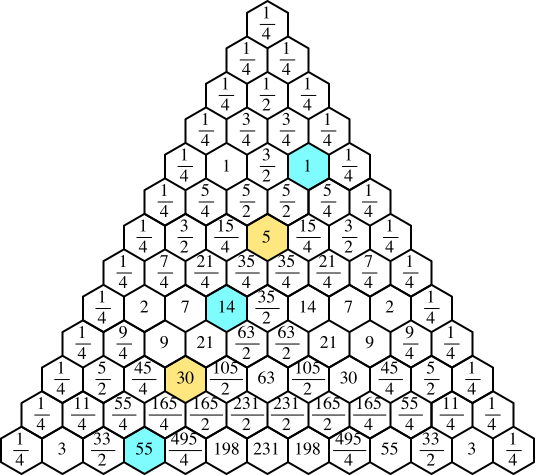
Abb. 6: Modifiziertes Pascal-Dreieck der Binomialkoeffizienten

Somit erhalten wir für die Summenfolge der Rösselsprung-Wege mit ungerader Startzahl n die explizite Formel:

s[n] = 1/4*binomial(n+3, 3)

Beweisskizze: Die Multiplikationstabelle ist quadratischer Natur, wir haben Produkte mit zwei Faktoren. Summen auf parallelen geradlinigen Anordnungen sind daher arithmetische Folgen dritter Ordnung. Im Pascal-Dreieck bilden die Einträge auf einer dritten Schrägzeile ebenfalls eine arithmetischen Folge dritter Ordnung. Wenn wir bei zwei arithmetischen Folgen dritter Ordnung vier übereinstimmende Folgenglieder haben, sind die beiden Folgen gleich.

5 Gerade Startzahlen

Die Abbildung 7 zeigt das Entsprechende für gerade Startzahlen.

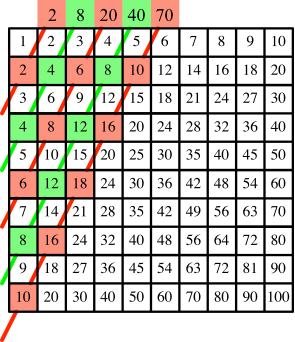
Abb. 7: Gerade Startzahlen

Wir erhalten die Summenfolge 2, 8, 20, 40, 70, ... .

Auch diese Folge finden wir in einem modifizierten Pascal-Dreieck: die Einträge werden verdoppelt. Die dritte Schrägzeile ist unsere Summenfolge.

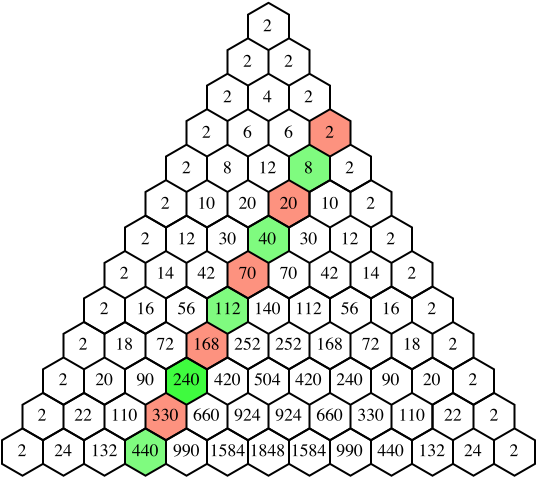
Abb. 8: Verdoppelung der Binomialkoeffizienten

Somit erhalten wir für die Summenfolge der Rösselsprung-Wege mit gerader Startzahl n die explizite Formel:

s[n] = 2*binomial(n/2+2, 3)

6 Differenzenfolgen

Die Summenfolge 1, 5, 14, 30, 55, ... (ungerade Startzahl) hat die Differenzenfolge 4, 9, 16, 25, ... , also die Quadratzahlen.

Die Summenfolge 2, 8, 20, 40, 70, ... (gerade Startzahl) hat die Differenzenfolge 6, 12, 20, 30, ... . Diese Zahlen haben die Form n*(n+1).

Diese Zahlen finden sich auch in den Ecken der Ulam-Spirale (Abb. 9).

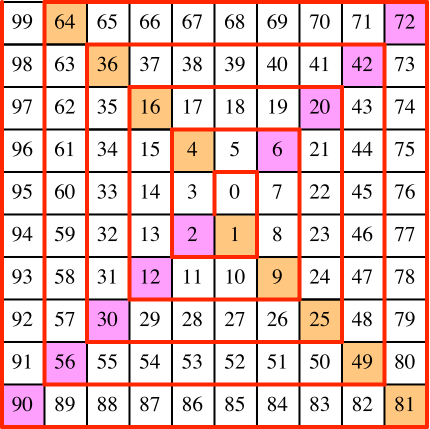
Abb. 9: Ulam-Spirale

Weblink

The On-Line Encyclopedia of Integer Sequences® (OEIS®)

https://oeis.org/

https://oeis.org/search?q=1%2C2%2C5%2C8%2C14%2C20%2C30%2C40%2C55&language=english&go=Search

Hans Walser: Verschränkung

https://walser-h-m.ch/hans/Miniaturen/V/Verschraenkung/Verschraenkung.html

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).