Hans Walser, [20160703]
Eckiger Hippokrates
1 Worum geht es?
Es wird ein Flchensatz gezeigt, der eine spezielle Verallgemeinerung der ãMndchen des HippokratesÒ darstellt. Der Flchensatz gestattet einen Zerlegungsbeweis.
2 Abnderung der Pythagoras-Ikone
In der Regel werden bei der Pythagoras-Ikone die drei Quadrate nach au§en angesetzt. Wir setzen nun das Hypotenusenquadrat nach innen an (Abb. 1).
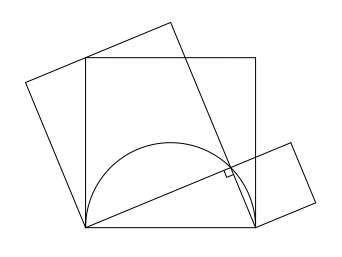
Abb. 1: Abgenderte Pythagoras-Ikone
Die linke obere Ecke des Hypotenusenquadrates liegt tatschlich auf einer Seite des linken Kathetenquadrates.
3 Ein Flchensatz
Die rot bemalten Flchen sind zusammen gleich gro§ wie die blau bemalten Flchen (Abb. 2).
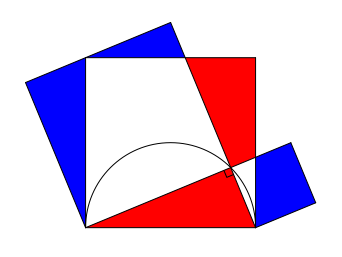
Abb. 2: Rot = Blau
Beweis: Es ist:
Hypotenusenquadrat = Wei§ plus Rot
Kathetenquadrate zusammen = Wei§ plus Blau
Da nach dem Satz des Pythagoras die Kathetenquadrate zusammen gleich gro§ sind wie das Hypotenusenquadrat, ist Rot gleich Blau.
Fr Verallgemeinerungen siehe (Heinrich / Schmitz / Walser, 1999).
4 Zerlegungsbeweis
Wir zeigen hier einen einfachen Zerlegungsbeweis (Abb. 3).

Abb. 3: Zerlegungsbeweis
5 Fnfecke
Anstelle von Quadraten setzen wir regelm§ige Fnfecke an (Abb. 4).
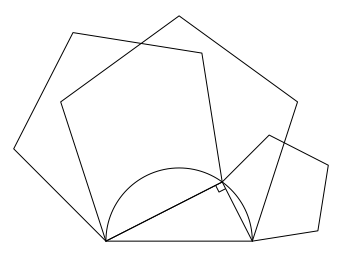
Abb. 4: Regelm§ige Fnfecke
Wieder entsteht nach (Heinrich / Schmitz / Walser, 1999) ein Flchensatz (Abb. 5).
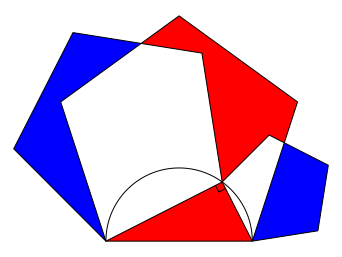
Abb. 5: Rot = Blau
Wir knnen wieder wie oben mit den Quadraten argumentieren, da der Satz des Pythagoras auch fr angesetzte regelm§ige Fnfecke gilt.
Ich habe keinen schnen Zerlegungsbeweis gefunden.
Literatur
Heinrich, Frank / Schmitz, Michael / Walser, Hans (1999): Verallgemeinerungen der ÒMndchen des HippokratesÓ. MNU Der mathematische und naturwissenschaftliche Unterricht 52/5, 1999, 264-270.