Hans Walser, [20180330]
Dritteln mit Origami
1 Worum geht es?
Mit einer Einschiebe-Methode kann die Seite eines Origami-Papiers gedrittelt werden. Verallgemeinerung.
2 Dritteln
2.1 Faltvorgang
Wir markieren den Mittelpunkt der linken Seite (kann durch Falten ermittelt werden) und die untere Seite rot, die Ecke rechts unten und die obere Seite blau (Abb. 1a).
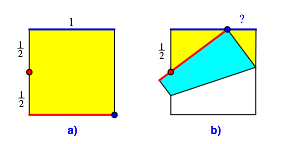
Abb. 1: Faltvorgang
Nun falten wir so, dass die rote Seite auf den roten Punkt und der blaue Punkt auf die blaue Seite zu liegen kommen (Abb. 1b). Die kurze blaue Strecke ist dann ein Drittel der blauen Seite des Origami-Papiers.
2.2 Beweis durch Rechnen
Wir verwenden die Bezeichnungen der Abbildung 2.
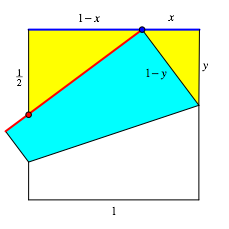
Abb. 2: Daten und Bezeichnungen
Aus der €hnlichkeit der beiden gelben Dreiecke folgt:
![]() (1)
(1)
Der Satz des Pythagoras gibt fŸr das rechtwinklige gelbe Dreieck rechts oben:
![]() (2)
(2)
Gleichsetzen von (1) und (2) ergibt die quadratische Gleichung:
![]() (3)
(3)
Die quadratische Gleichung (3) hat die beiden Lšsungen:
![]() (4)
(4)
TatsŠchlich ist auch die erste Lšsung richtig (Abb. 3). Sie ist ein Grenzfall des Faltprozesses.
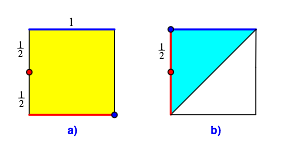
Abb. 3: Illustration der ersten Lšsung
Die Abbildung 4 gibt weitere Daten zur zweiten Lšsung.
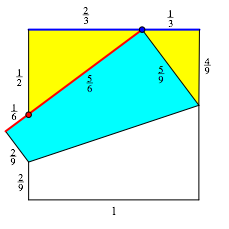
Abb. 4: Weitere Daten
Die beiden gelben rechtwinkligen Dreiecke haben das SeitenverhŠltnis 3:4:5, sind also ãLehrerdreieckeÒ (einfachstes pythagoreisches Dreieck).
2.3 Klassische Methode
Zur Erinnerung: Die Abbildung 5 illustriert die klassische Methode der Seitendrittelung. Es braucht sehr viel mehr Faltlinien, dafŸr kann der Beweis linear gefŸhrt werden.
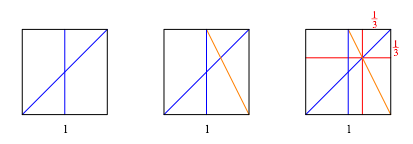
Abb. 5: Klassische Methode
3 Verallgemeinerung
Die Abbildung 6 illustriert eine Verallgemeinerung.
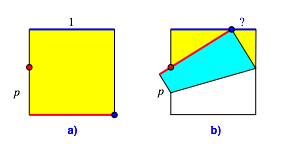
Abb. 6: Verallgemeinerung
Mit den zur Abbildung 2 analogen Bezeichnungen finden wir:
![]() (5)
(5)
Diese Zuordnung hat es in sich. Es ist nŠmlich:
![]() (6)
(6)
Das ãZurŸckkommenÒ kann wie folgt mit Falten illustriert werden.
Wir bringen am linken Rand eine Faltmarke an (Abb. 7a). Die Faltmarke hat den Vorteil, dass sie auf beiden Seiten des Papiers sichtbar ist. Und nun falten wir wie gehabt, also die untere Quadratseite auf die rote Marke und die rechte untere Quadratecke auf die Oberseite des Quadrates. Wir bringen am oberen Rand eine weitere Faltmarke gemŠ§ Abbildung 7b an. Das ist der Ort, wo die rechte untere Quadratecke auf der Oberseite ankommt.
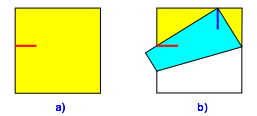
Abb. 7: Erster Schritt
Wir falten auf (Abb. 8a) und wenden das Papier um die von links oben nach rechts unten laufende Diagonale (Abb. 8b).
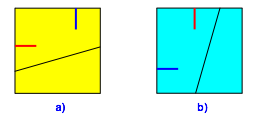
Abb. 8: Auffalten und Umwenden
Nun falten wir mit vertauschten Rollen (Abb. 9a) und stellen fest, dass die rechte untere Quadratecke genau bei der roten Marke ankommt. Dies ist das ãZurŸckkommenÒ.
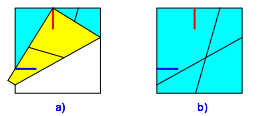
Abb. 9: Falten mit vertauschten Rollen
Wir falten wieder auf (Abb. 9b).
Vermutungen (Abb. 10):
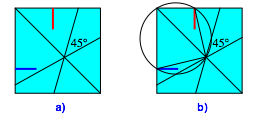
Abb. 10: Vermutungen
Die beiden Faltlinien schneiden sich unter einem Winkel von 45¡.
Der Schnittpunkt liegt auf der von links oben nach rechts unten laufenden Quadratdiagonale.
Der Schnittpunkt der Faltlinien, die beiden Faltmarken und eine Ecke des Quadrates liegen auf einem Kreis.