Hans Walser, [20140924]
Drittel-Linien
Anregung: A. K., V.
1 Worum geht es?
Im Viereck halbieren sich die Mittenlinien gegenseitig. Diese Eigenschaft wird verallgemeinert.
2 Mittenlinien
Im Viereck halbieren sich die Mittenlinien gegenseitig (Abb. 1a).
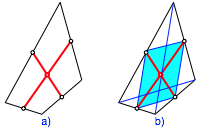
Abb. 1: Mittenlinien halbieren sich
Der Beweis lŠuft so: Die Seitenmitten des Viereckes bilden ein Parallelogramm, dessen Seiten parallel zu den Viereckdiagonalen sind.
3 Drittel-Linien
Die Drittel-Linien dritteln sich gegenseitig (Abb. 2). Beweis?

Abb. 2: Drittel-Linien
4 Sonderfall Trapez
Im Sonderfall eines Trapezes ergibt sich die Drittel-Eigenschaft aus den StrahlensŠtzen (Abb. 3).
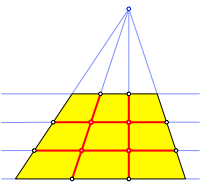
Abb. 3: Sonderfall Trapez
5 Zehntel-Linien
Die Abbildung 4 zeigt Zehntel-Linien, garniert mit Parallelogrammen.
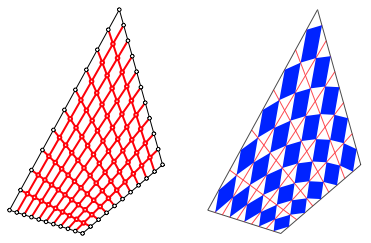
Abb. 4: Zehntel-Linien
6 Beweis fźr den allgemeinen Fall
Wir teilen zwei gegenźberliegende Seiten des Vierecks im VerhŠltnis λ, die beiden anderen Seiten im VerhŠltnis μ. Wir verbinden dann die Teilpunkte gegenźberliegender Seiten. Zu zeigen ist: diese Verbindungslinien teilen sich gegenseitig in den VerhŠltnissen λ und μ.
Wir verwenden die Bezeichnungen der Abbildung 5.
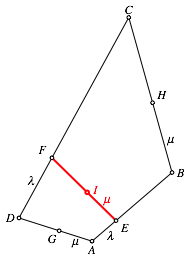
Abb. 5: Bezeichnungen
ZunŠchst teilen wir die Seiten AB und DC im gleichen VerhŠltnis λ. Es ist also:
![]()
In der Abbildung 4 ist λ = 0.3.
Dann teilen wir die Strecken AD, BC und EF im gleichen VerhŠltnis μ:
![]()
In der Abbildung 4 ist μ = 0.45.
Zu zeigen ist: Die Strecke GH wird durch die Strecke EF in I geschnitten und im VerhŠltnis λ geteilt, also:
![]()
Das ist eine Vektorerei. Es ist:
![]()
Weiter ist:
![]()
Und weiter:
![]()
Somit ist:
![]()
Dies war zu beweisen.
7 Viereckraster
Fźr ganze Zahlen λ und μ erhalten wir ein Viereckraster wie folgt. Wir verlŠngern die Viereckseiten und tragen Vielfache der SeitenlŠngen ab (Abb. 6).

Abb. 6: Erster Schritt
Anschlie§end ergŠnzen wir zum Viereckraster (Abb. 7).

Abb. 7: Viereckraster
Jede Rasterlinie der einen Schar wird von den Rasterlinien der anderen Schar in gleichmŠ§igen AbstŠnden geschnitten. Deshalb handelt es sich nicht um ein so genanntes Moebius-Netz, also ein projektives Bild des Quadratrasters.
Wir sehen, dass sich beim †berschneiden der Linien was Spannendes anbahnt.
8 Parabel
Wenn wir das Viereckraster fortsetzen, źberschneiden sich die Rasterlinien. Als Enveloppe entsteht eine Parabel (Abb. 8). Beweis weggelassen.

Abb. 8: Parabel
Ein Kegelschnitt ist durch fźnf tangentiale Geraden festgelegt. In unserem Fall sind das die vier Viereckseiten und die unendlich ferne Gerade.