1 Worum geht es?

Durch iterierte Unterteilung eines rechtwinkligen Dreiecks durch die Höhe kommen wir zu den Binomialkoeffizienten und der Binomialverteilung.

2 Unterteilung des rechtwinkligen Dreiecks

Ein Dreieck wird durch eine Ecktransversale in zwei Teildreiecke zerlegt (Hölzl 2017). Dabei können verschiedene Bedingungen an das Startdreieck und die beiden Teildreiecke gestellt werden.

Wir besprechen den Sonderfall eines rechtwinkligen Dreiecks, welches wir durch die Höhe in zwei Teildreiecke zerlegen. Die beiden Teildreiecke sind wieder rechtwinklig. Sie sind zueinander gleichsinnig ähnlich und zum Startdreieck ungleichsinnig ähnlich.

3 Iteration

Dann iterieren wir den Zerlegungsvorgang.

4 Schritt für Schritt

Erster Schritt: Wir unterteilen das rechtwinklige Startdreieck mit der Höhe in zwei Teildreiecke (Abb. 1). In der üblichen Notation für das rechtwinklige Dreieck (Katheten und , Hypotenuse ) haben die beiden Teildreiecke gegenüber dem Startdreieck die Längenverkleinerungsfaktoren beziehungsweise . Die Flächenverkleinerungsfaktoren sind entsprechend und . Es wird sich bald als sinnvoll erweisen, mit den beiden Abkürzungen und zu arbeiten. Der Satz des Pythagoras liefert . Das am Rande.

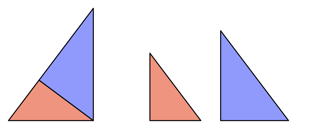
Abb. 1: Unterteilung mit der Höhe. Teildreiecke

Zweiter Schritt: Und nun kommt das Entscheidende. Wir unterteilen auch die beiden Teildreiecke mit ihren Höhen (Abb. 2).

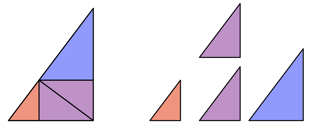
Abb. 2: Wiederholung des Unterteilens. Teildreiecke

Das gibt zunächst vier Teildreiecke. Allerdings ist aus Symmetriegründen sofort klar, dass die beiden mittleren gleich groß sind. Das eine der beiden mittleren lila Dreiecke ist dabei das große Teildreieck vom vorhergehenden kleinen Teildreieck, und das andere das kleine Teildreieck vom vorhergehenden großen Teildreieck.

Die Flächenverkleinerungsfaktoren sind der Reihe nach einmal , zweimal und schließlich einmal . Die zweimaligen Faktoren sind genau genommen einmal und einmal . Wer in der Schule einen Fensterplatz hatte, sieht, worauf das hinausläuft. Fügen wir noch zwei weitere Schritte an.

Dritter Schritt: Die Abbildung 3 zeigt die nächste Unterteilung.

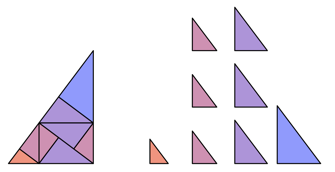
Abb. 3: Dritter Schritt

Die acht Teildreiecke lassen sich der Größe nach klassifizieren. Die Flächenverkleinerungsfaktoren sind einmal , dreimal , dreimal und einmal .

Vierter Schritt: Die Abbildung 4 illustriert die vierte Unterteilung.

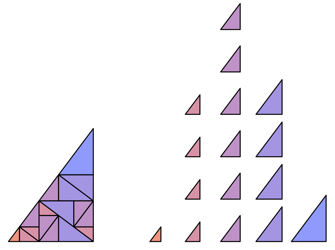
Abb. 4: Vierter Schritt

5 Feststellungen

Die Anzahlen der Dreiecke in den einzelnen Größenklassen sind die Binomialkoeffizienten. Für die ersten vier Unterteilungsschritte haben wir diese Klassifizierung mit Symmetrie- und Kongruenzüberlegungen nachgewiesen.

Für den allgemeinen Fall gilt folgende Rekursionsüberlegung. Jedes Teildreieck der Zerlegung nach Schritten wird im nächsten Schritt in ein kleines und ein großes Teildreieck zerlegt, wobei die beiden Faktoren und wechselseitig zum Tragen kommen. Daraus ergibt sich durch Zusammenfassen für die Anzahlen gleich großer Teildreiecke die übliche Rekursionsformel:

Für den Flächenanteil aller Dreiecke einer bestimmten Größenklasse gilt:

Déjà-vu. Hat hier allerdings gar nichts mit Glücksspielen zu tun.

6 Didaktisches

In der Schule werden die Binomialkoeffizienten oft mit Glücksspielen eingeführt (Glötzner 2017). Man kann dann auch sehr einfach zur Binomialverteilung und zum Erwartungswert übergehen. Dabei kann auch das lebensweltliche Problem der Spielsucht thematisiert werden.

Literatur

Glötzner, Fabian (2017): Binomialverteilung erkunden. Beispiele untersuchen, systematisieren und erweitern. mathematik lehren 201 | 2017, 36-41.

Hölzl, Reinhard (2017): Dreiecke in Dreiecke zerlegen. Welche Eigenschaften und Zusammenhänge findest du? mathematik lehren 201 | 2017, 12-15.