Hans Walser, [20230909]
Dreieck und Quadrat
1 Worum es geht
Gemeinsame Zerlegungen von flächengleichen gleichseitigen Dreiecken und Quadraten. Exemplarisches Vorgehen.
Im Folgenden ein Überblick.
1.1 Konstruktion
Zunächst stellt sich die Frage, wie zu einem gegebenen Quadrat ein flächengleiches gleichseitiges Dreieck mit den Methoden der Euklidischen Geometrie (Zirkel und Lineal) konstruiert werden kann. Die präsentierte Konstruktion (Abb. 1.1 und 1.2) basiert auf den Strahlensätzen und dem Höhensatz.
1.2 Puzzle
Die einzelnen Teile der gemeinsamen Zerlegung werden gegeben, dazu die Rahmenfiguren von Quadrat und Dreieck (Abb. 2.1 und 2.2). Mit den Einzelteilen sollen einerseits das Quadrat und andererseits das Dreieck belegt werden.
1.3 Weitere Beispiele
In etlichen der vorgestellten Beispiele (Abb. 3.1, 3.2, 3.4) und der gegebenen Anordnung der Rahmenfiguren können die Einzelteile durch Translationen oder durch Punktspiegelungen (Translation und „auf den Kopf stellen“) von der einen Rahmenfigur in die andere übergeführt werden. Das Puzzle wird erleichtert, wenn die Einzelteile schon in der passenden Orientierung relativ zu den Rahmenfiguren gegeben sind. Schwieriger wird es, wenn die Einzelteile vorerst drucheinandergewirbelt werden.
Das Vorgehen kann mit ausgeschnittenen Papier-Einzelteilen und auf Papier ausgedruckten Rahmenfiguren erfolgen. Einfacher ist ein digitales Vorgehen am Bildschirm. Sinnvoll ist es, mit einer Software zu arbeiten, welche ein haptisches (also mit Mausbewegung gesteuertes) Verschieben der Einzelteile erlaubt. Der Autor hat mit EazyDraw gearbeitet. GeoGebra benötigt für jede Verschiebung die vorgängige Definition des Verschiebungsvektors und ist daher für unser Problem wenig geeignet.
In zwei Beispielen braucht es zusätzlich Achsenspiegelungen (Abb. 3.3 und 3.5). Kombiniert mit einer Translation ist das eine Schubspiegelung.
Der Sinn dieser Puzzle-Aktivitäten besteht in der geometrischen Mustererkennung, der mentalen Bewegung von Figuren und der Organisation von Figuren in der Ebene.
1.4 Analyse
Ein vorgegebenes Puzzle kann oder muss auf Stimmigkeit überprüft werden (Abb. 4.1 bis 4.5). Es könnte sich ja auch um eine Näherungslösung handeln. Für die Analyse sind Methoden aus dem Bereich der flächeninvarianten Umformung von Figuren erforderlich.
1.5 Eigenbau
Das höchste der Gefühle ist natürlich die Kreation einer eigenen Zerlegung. Es wird exemplarisch das Vorgehen dazu gezeigt (Abb. 5.1 bis 5.13, Abb. 6).
2 Rechnung und Konstruktion
Zu einem gegebenen Quadrat ist ein flächengleiches gleichseitiges Dreieck gesucht.
2.1 Rechnung
Das gegebene Quadrat habe die Seitenlänge 1, das gesuchte Dreieck die Seitenlänge s. Die Flächengleichheit führt auf die Bedingung:
![]()
Daraus ergibt sich (man beachte die vierte Wurzel, eine Seltenheit in der Geometrie):
![]()
2.2 Konstruktion
Wir beginnen mit dem Quadrat und tragen außen einen Drittel der Seitenlänge ab gemäß Abbildung 1.1. Die Stimmigkeit der Konstruktion ergibt sich aus den Strahlensätzen.
Mit einem Thaleskreis erhalten wir eine Strecke der Länge:
![]()
Der Hintergrund ist der Höhensatz im rechtwinkligen Dreieck.
Mit einem zweiten Thaleskreis erhalten wir eine Strecke der Länge:
Dies ist die halbe Seitenlänge des gesuchten Dreiecks.
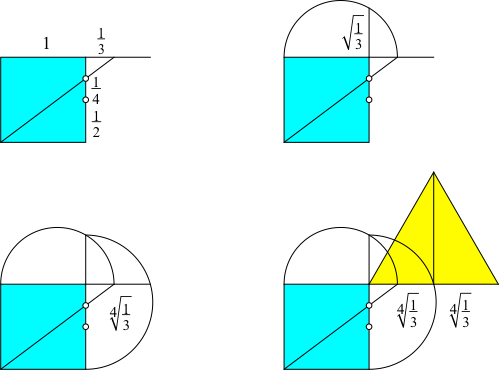
Abb. 1.1: Konstruktionsschritte
Die Abbildung 1.2 zeigt die Konstruktion im Überblick.
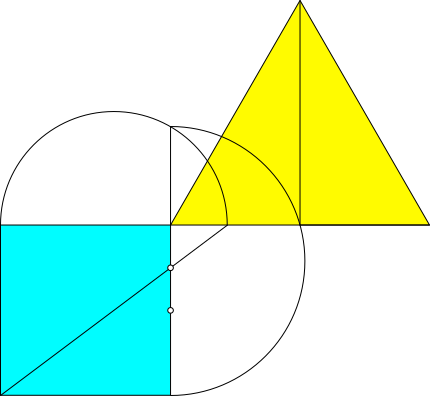
Abb. 1.2: Überblick
3 Puzzle
Die Puzzleteile (Abb. 2.1) passen sowohl in den Quadratrahmen wie auch in den Dreiecksrahmen (Abb. 2.2).

Abb. 2.1: Puzzleteile
Abb. 2.2: Quadrat- und Dreieckrahmen
Die Teile sind bereits passend orientiert. Für das Quadrat können sie direkt eingeschoben werden, die Teile müssen also nicht mehr verdreht werden.
Für das Dreieck können die Teile der oberen Reihe (gelb, rot, blau und hellblau) ebenfalls direkt eingeschoben werden. Die Teile der unteren Reihe (magenta, grün, orange), müssen vor dem Einschieben auf den Kopf gestellt werden, das heißt um 180° gedreht werden. (Die Abbildung 3.2 zeigt eine Lösung.)
4 Beispiele von gemeinsamen Zerlegungen
Die Abbildungen 3.1 bis 3.5 zeigen Beispiele von gemeinsamen Zerlegungen. Es gibt unendlich viele Beispiele.
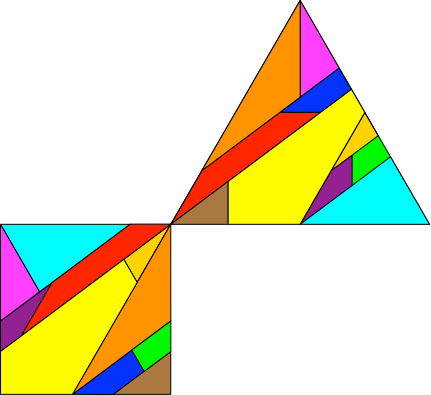
Abb. 3.1: Beispiel
Das Beispiel der Abbildung 3.2 zeigt eine Lösung des Puzzles der Abbildungen 2.1 und 2.2.
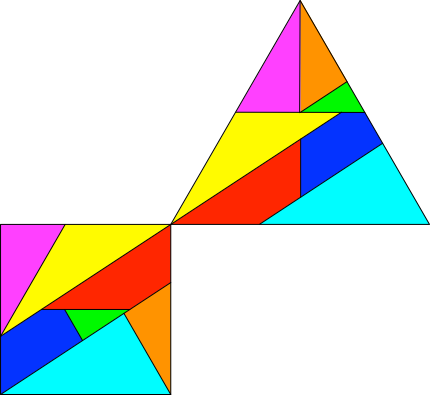
Abb. 3.2: Beispiel
Im Beispiel der Abbildung 3.3 gibt es Einzelteile (gelb und braun), welche beim Übergang vom Quadrat zum Dreieck an einer horizontalen Achse gespiegelt werden müssen. Sind die Einzelteile auf Papier gegeben, müssen sie gewendet werden.
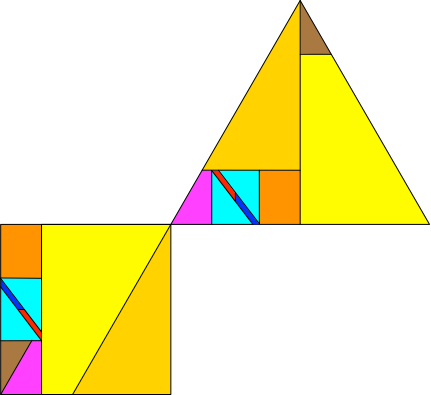
Abb. 3.3: Beispiel
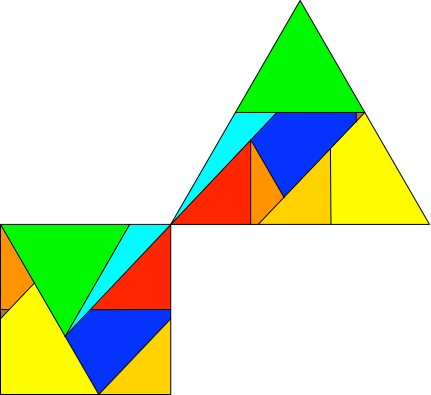
Abb. 3.4: Beispiel
Auch im Beispiel der Abbildung 3.5 müssen Einzelteile (braun und magenta) an einer horizontalen Achse gespiegelt werden.
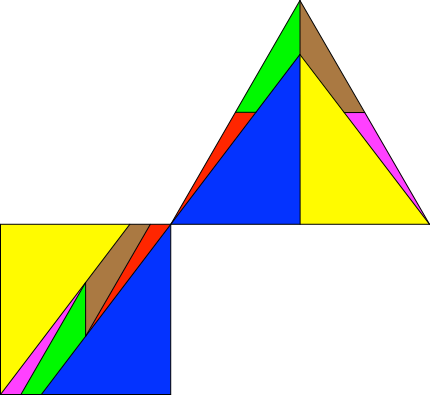
Abb. 3.5: Beispiel
5 Analyse eines Beispiels
Wir analysieren das Beispiel der Abbildung 3.1. Das Vorgehen ist destruktiv.
Die Abbildung 4.1 zeigt nochmals die Ausgangslage.
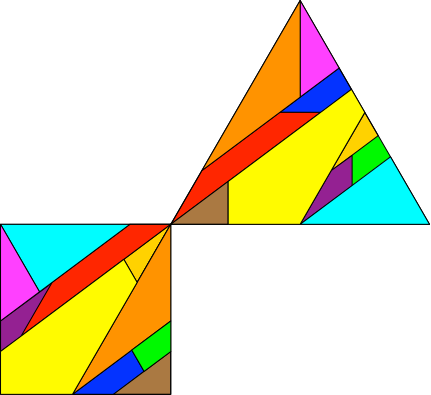
Abb. 4.1: Ausgangslage
Nun schneiden wir das gleichseitige Dreieck und das Quadrat so zurecht, dass wir nach Anfügen der abgeschnittenen Teile zwei Parallelogramme mit parallelen Seiten und daher gleichen Winkeln haben (Abb. 4.2). Im vorliegenden Beispiel haben wir zwei Parallelogramme mit spitzen Winkeln 60°. Durch Vergleich mit der Ausgangslage (Abb. 4.1) sehen wir, was wo abgeschnitten und wieder angesetzt wird.
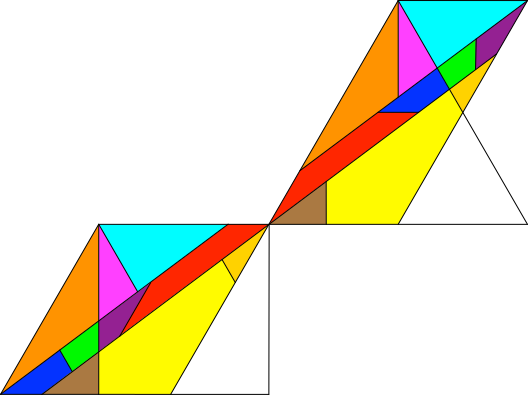
Abb. 4.2: Umformen der beiden Figuren.
Es läuft nun wie auf Schienen. Das rote Trapez ist offensichtlich. Daneben haben wir je ein blau-grün-lila Trapez, das zum roten Trapez kongruent ist (punktgespiegelt) und auf denselben Schienen läuft. Das orange-magenta-hellblaue Dreieck finden wir ebenfalls auf derselben Schiene. Ebenso das braun-gelb-goldene Dreieck. Dieses ist kongruent zum orange-magenta-hellblauen Dreieck (Punktspiegelung).
Durch dieses Zusammenfassen von Teilfiguren haben wir nur noch zwei Formen, das Trapez und das Dreieck. In der Abbildung 4.3 sind diese Formen blaugrau umrandet.
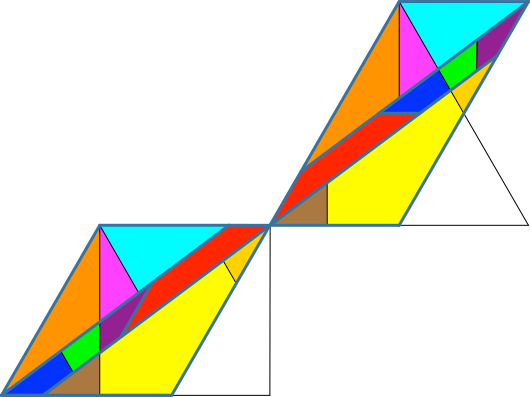
Abb. 4.3: Zusammenfassen zu Formen
Die Abbildung 4.4 beschränkt sich auf diese Formen.
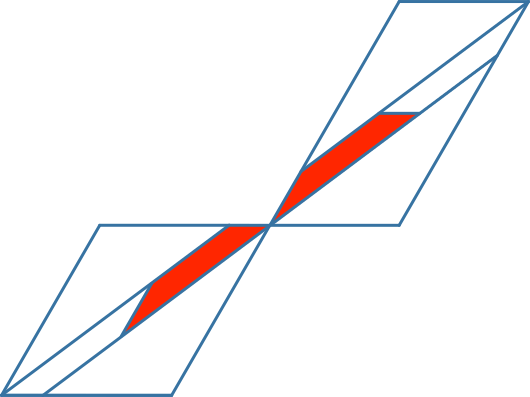
Abb. 4.4: Zwei Formen
Die Zerlegungsgleichheit kann durch Neufärben offensichtlich gemacht werden (Abb. 4.5).

Abb. 4.5: Die Zerlegungsgleichheit ist offensichtlich
6 Konstruktives Vorgehen
Wir wollen nun selber eine gemeinsame Zerlegung bauen. Wir beginnen mit einem Quadrat und einem flächengleichen gleichseitigen Dreieck (Abb. 5.1).
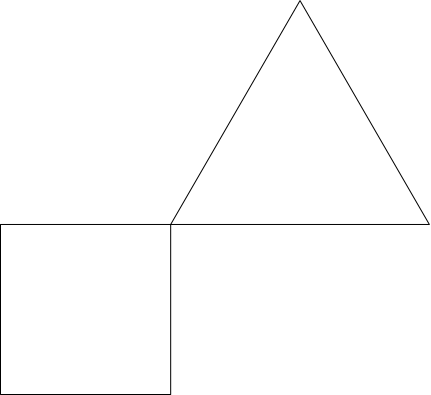
Abb. 5.1: Quadrat und flächengleiches gleichseitiges Dreieck
Nun formen wir die beiden Figuren so um, dass die Flächen erhalten bleiben, wir aber zwei Parallelogramme mit gleichen Winkeln erhalten. Die Abbildung 5.2 zeigt eine mögliche Lösung.
Da wir die gemeinsamen Winkel der beiden Parallelogramme beliebig wählen können, gibt es unendlich viele Lösungen. Am einfachsten ist es, bereits in den Startfiguren vorkommende Winkel zu wählen, in unserem Fall also Winkel von 60° oder 90°.
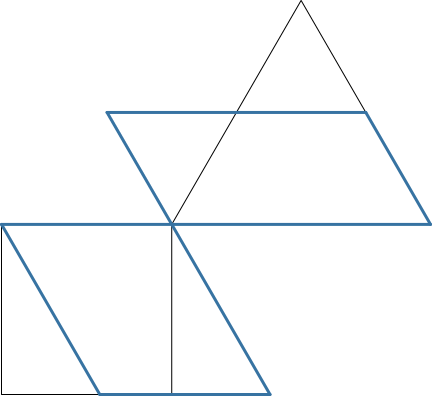
Abb. 5.2: Parallelogramme
Interessanterweise können wir nun drei parallele Linien einzeichnen (orange in Abb. 5.3). Für den Nachweis der Parallelität verwenden wir einerseits die Flächen- und Winkelgleichheit der beiden Parallelogramme (wir erinnern uns an die Formel für die Parallelogramm-Fläche: Seite mal Seite mal Sinus des eingeschlossenen Winkels) und andererseits die Strahlensätze.
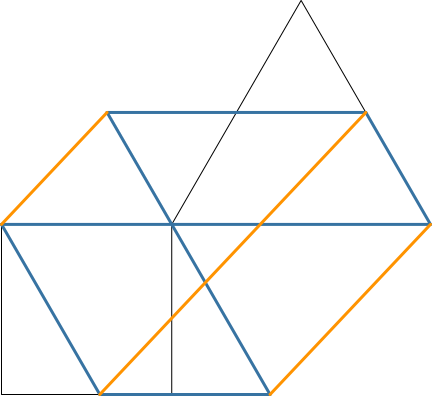
Abb. 5.3: Parallele Linien
Wir zeichnen noch eine vierte parallele Linie ein (Abb. 5.4). Damit ist unser Schienensystem komplett.
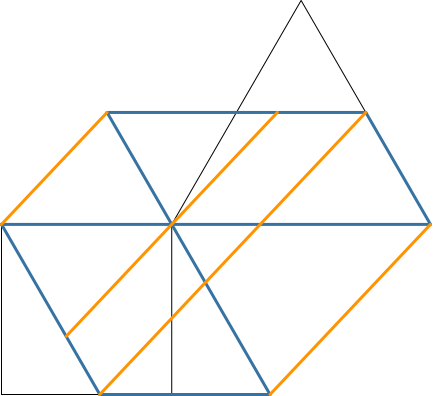
Abb. 5.4: Verschiebebahnhof
Die Idee ist nun, eine gemeinsame Zerlegung der beiden Parallelogramme zu finden. Wir sehen sofort kongruente Dreiecke, die wir hin- und herschieben können (gelb in Abb. 5.5).

Abb. 5.5: Kongruente Dreiecke
Leider bleiben zwei kleine Parallelogramme übrig (grau in Abb. 5.6), welche zwar flächengleich sind, aber nicht kongruent.
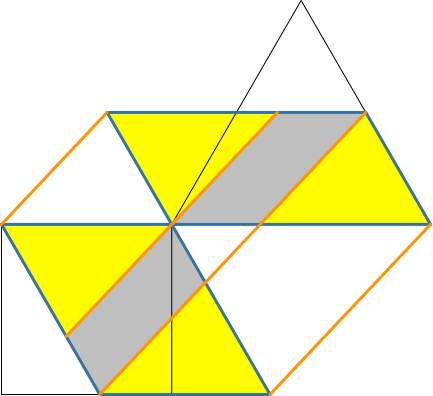
Abb. 5.6: Flächengleiche, aber nicht kongruente Rest-Parallelogramme
Wir halbieren jedes dieser beiden grauen Parallelogramme mit einem Schnitt durch den Mittelpunkt. Die Schnittrichtungen orientieren sich an den grauen Kanten der großen Parallelogramme (Abb. 5.7). Wir erhalten vier Trapeze, welche alle vier kongruent sind. Der Nachweis der Kongruenz ist eine kleine Denksportaufgabe.
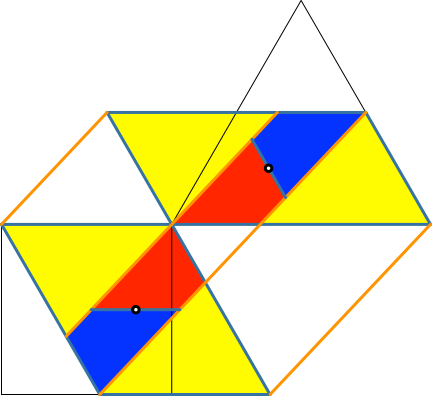
Abb. 5.7: Halbierung
Wir haben nun eine gemeinsame Zerlegung der beiden großen Parallelogramme gefunden.
Jetzt geht es noch darum, die Einzelteile zusätzlich so zu zerlegen, dass sie mit dem ursprünglichen Quadrat und dem gleichseitigen Dreieck kompatibel sind.
Wir können zunächst die beiden gelben Dreiecke links so zerlegen, dass sie mit dem gleichseitigen Dreieck kompatibel sind (grün und hellblau in Abb. 5.8).
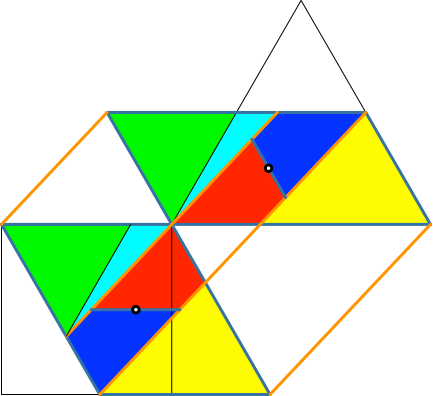
Abb. 5.8: Kompatibilität mit dem gleichseitigen Dreieck
Weiter können wir die gelben Dreiecke rechts auf Kompatibilität mit dem Quadrat trimmen (gold und wieder gelb in Abb. 5.9).
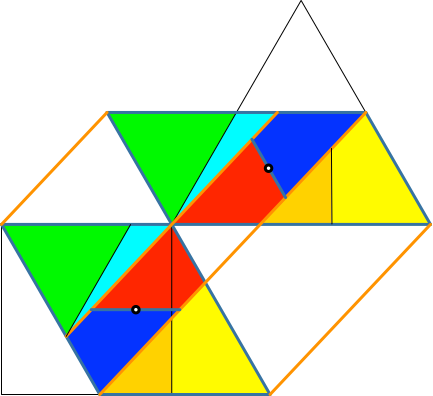
Abb. 5.9: Kompatibilität mit Quadrat
Auch die Trapeze müssen auf das Quadrat zugeschnitten werden (Abb. 5.10). Beim blauen Trapez ist ein ganz kleines Dreiecklein abzuschneiden.
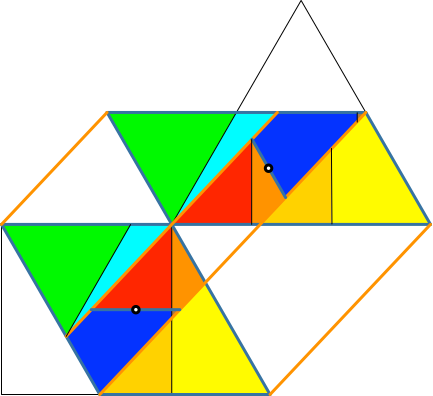
Abb. 5.10: Zuschneiden der Trapeze
Damit ist die gemeinsame Zerlegung kompatibel mit dem Quadrat und dem gleichseitigen Dreieck.
Jetzt muss die in der Abbildung 5.2 vorgenommene Umformung zu den großen Trapezen rückgängig gemacht werden. In der Abbildung 5.11 ist das gleichseitige Dreieck wieder vollständig.
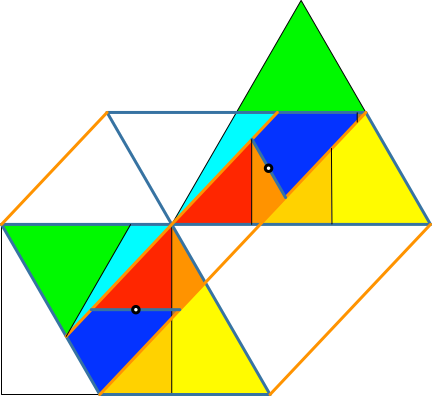
Abb. 5.11: Gleichseitiges Dreieck vollständig
In der Abbildung 5.12 ist auch das Quadrat restituiert worden.
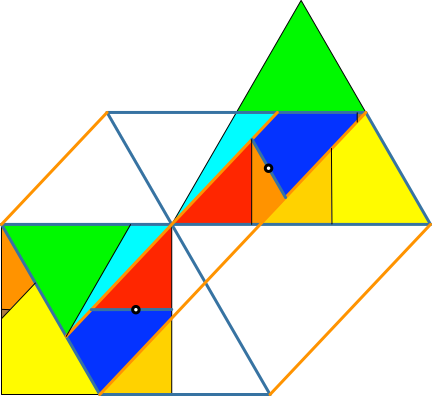
Abb. 5.12: Quadrat vollständig
Schließlich können wir die Hilfslinien abbauen (Abb. 5.13). Wir erhalten die gemeinsame Zerlegung. (Es handelt sich um des Beispiels 3.4).

Abb. 5.13: Gemeinsame Zerlegung von gleichseitigem Dreieck und Quadrat
Die Abbildung 6 zeigt die Konstruktion mit Zwischenschritten.
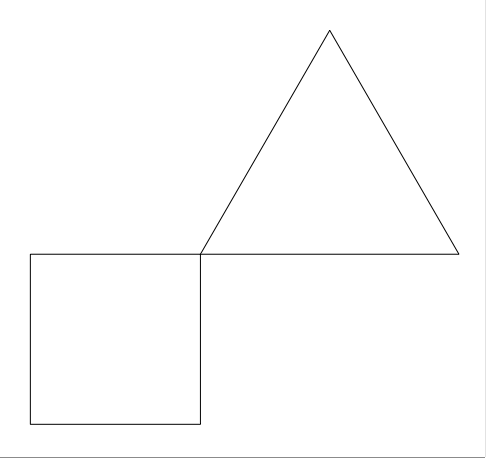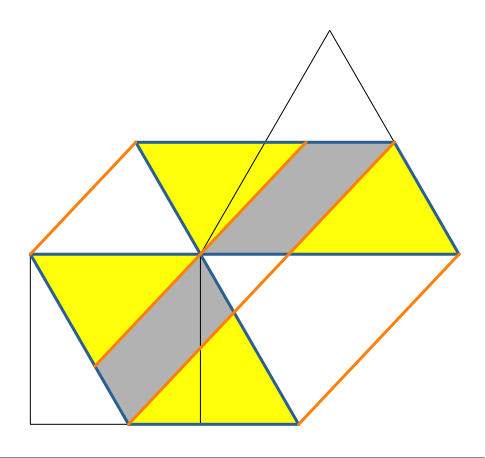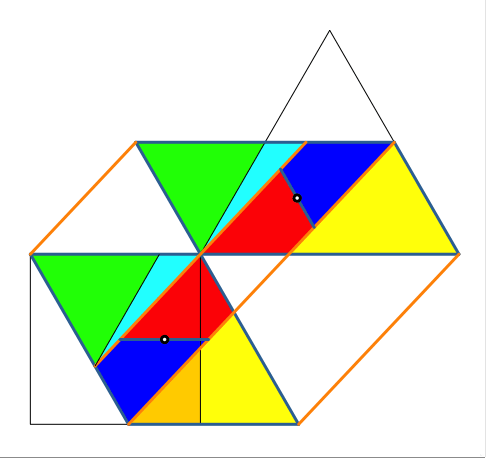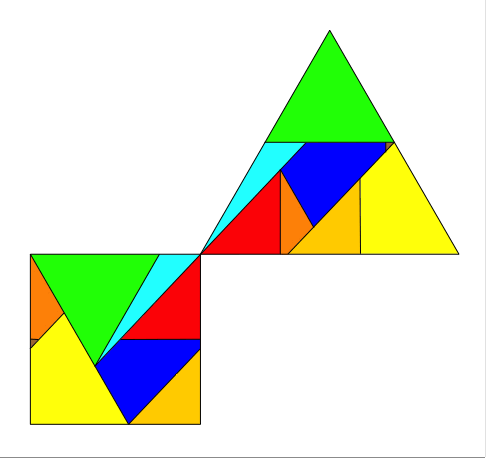
Abb. 6: Animation
Weblinks
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney/Dudeney.htm
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney2/Dudeney2.htm
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney3/index.html
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney4/index.html
Hans Walser: Dudeney
http://www.walser-h-m.ch/hans/Miniaturen/D/Dudeney5/index.html