Hans Walser, [20240203]
Drehung an Würfelkanten
1 Worum es geht
Wir drehen Ebenen um die Kanten eines Würfels.
2 Ausgangslage
Wir spannen je zwischen zwei durch eine Kante verbundene Würfelecken diagonal ein Quadrat ein (Abb. 1). Insgesamt also zwölf Quadrate.
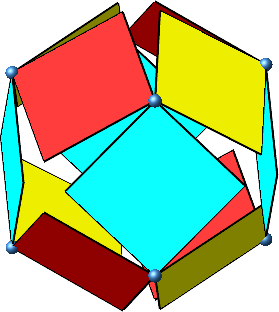
Abb. 1: Quadrate einspannen
In der Ausgangslage der Abbildung 1 haben die Ebenen der eingespannten Quadrate gegenüber den Würfelseiten einen Neigungswinkel von 45°. Damit kann in die Figur ein regelmäßiges Rhombendodekaeder eingepasst werden.
3 Bewegung
Nun drehen wir die eingespannten Quadrate um die Würfelkanten (Abb. 2).
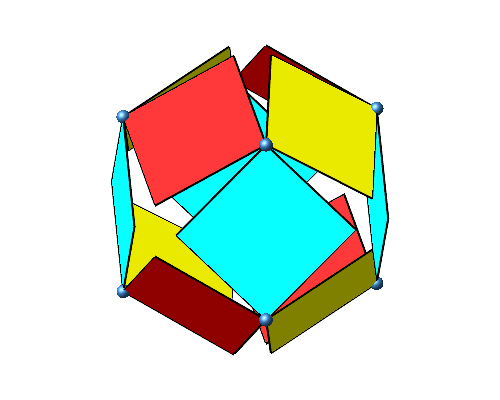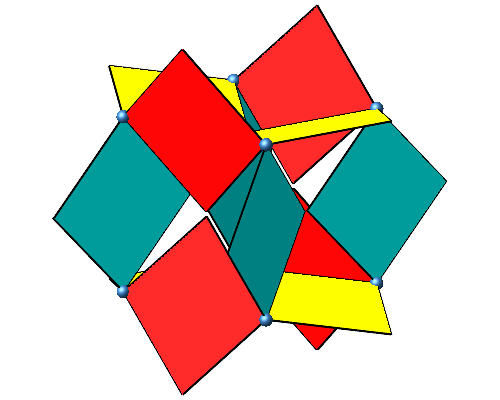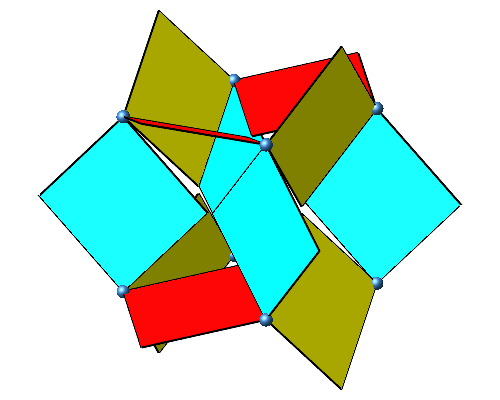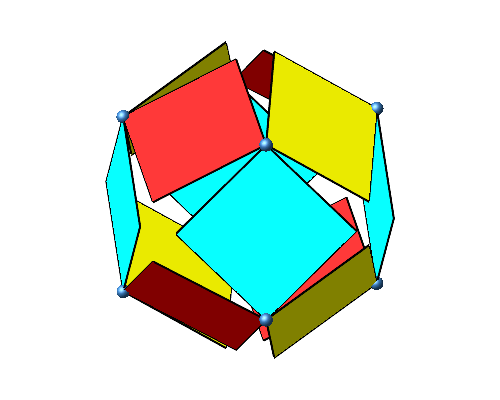
Abb. 2: Drehen der Quadrate
Der Drehsinn ist gleichmäßig verteilt. Wenn wir zum Beispiel vom Eckpunkt vorne oben Mitte je in Richtung einer der drei Würfelkanten gucken, haben wir immer einen positiven Drehsinn. Bei jeder zweiten Ecke haben wir ausschließlich einen positiven Drehsinn, bei den anderen Ecken einen negativen.
Der Sinn der vorliegenden Studie war für mich, diesen Drehprozess sichtbar zu machen.
4 Spezielle Positionen
Nach einer Drehung um 45°–arctan(1/Φ) ≈ 13.283° (dabei ist Φ = (1 + √5)/2 ≈ 1.618 der Goldene Schnitt) ist die Situation so, dass ein regelmäßiges Dodekaeder eingepasst werden kann (Abb. 3).
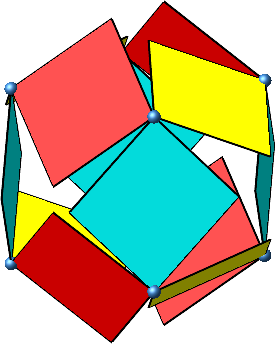
Abb. 3: Es kann ein regelmäßiges Dodekaeder eingepasst werden
Nach einer Drehung um 45° sind je zwei Quadrate in einer Ebene (Abb. 4). Es kann ein Würfel einpasst werden (eben der Würfel mit den gegebenen Ecken).
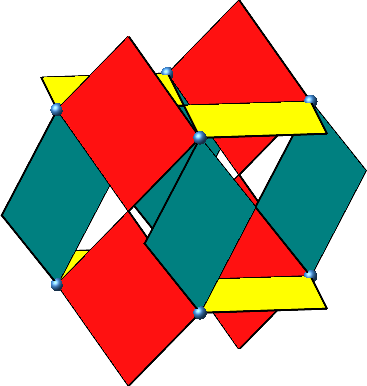
Abb. 4: Drehung um 45°
Nach einer Drehung um 90° verlaufen alle Quadratebenen durch den Würfelmittelpunkt (Abb. 5).
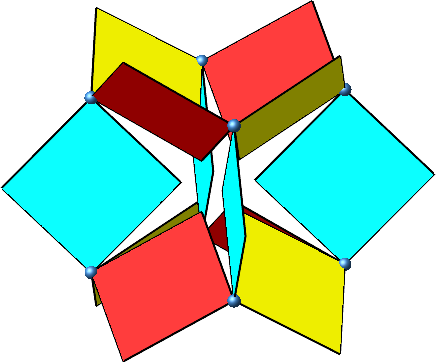
Abb. 5: Orientierung am Würfelmittelpunkt
Nach einer Drehung um 135° haben wir wiederum je zwei Quadrate in einer Ebene (Abb. 6). Die Situation ist aber anders als in der Abbildung 4.
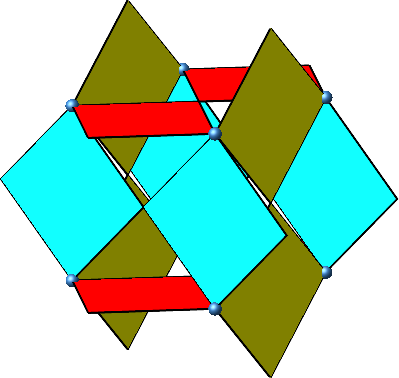
Abb. 6: Drehung um 135°
5 Isometrische Darstellung
Die Abbildung 7 zeigt die Drehungen aus der Sicht längs einer Raumdiagonalen des Würfels.
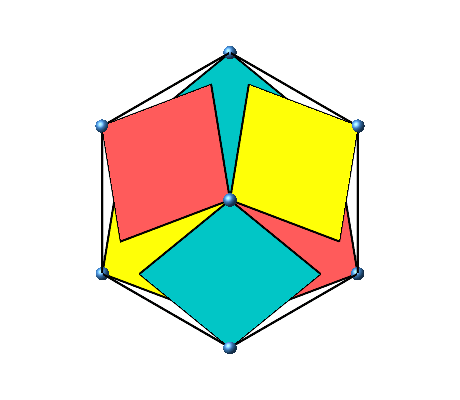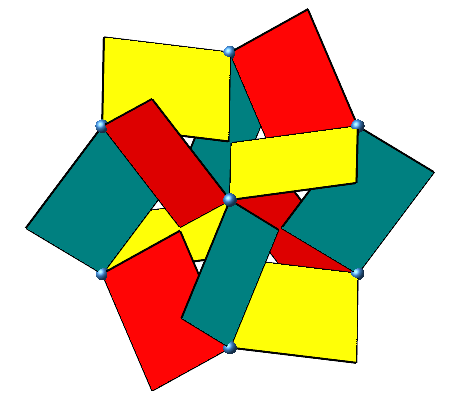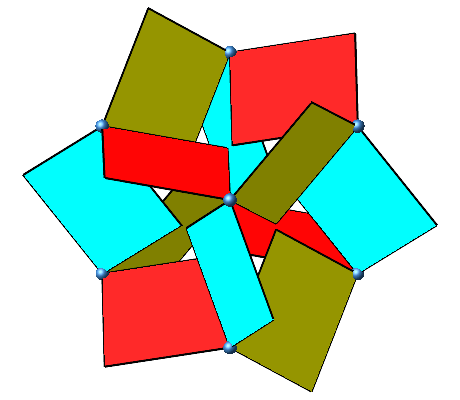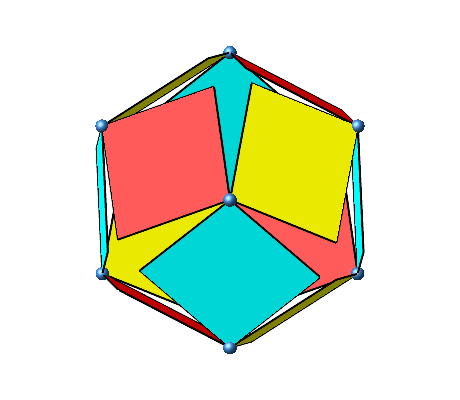
Abb. 7: Sicht längs einer Raumdiagonalen des Würfels
6 Mechanische Realisierung
Die Drehungen können mechanisch mit Kegelrädern realisiert werden. An jeder Würfelecke braucht es vier Kegelräder; je eines auf jeder Drehachse (Würfelkanten) sowie ein viertes zwischen diesen drei Kegelrädern, das in diese drei Kegelräder eingreift. Die Achse dies vierten Kegelrades ist eine Raumdiagonale des Würfels.
Weblinks
Hans Walser: Dodekaeder-Transformation
https://walser-h-m.ch/hans/Miniaturen/D/Dodekaeder-Transformation/Dodekaeder-Transformation.html