Hans Walser, [20230744]

Dodekaeder

1 Worum es geht

Dokumentation über das regelmäßige Dodekaeder

Figuren im Gerüst des regelmäßigen Dodekaeders und seiner Diagonalen

2 Koordinaten

Phi = Φ = (1+ √5)/2 (Goldener Schnitt)
phi = 1/ Φ = (–1+ √5)/2

A[0] := [0, 0, 0]: (Mittelpunkt, Ursprung des Koordinatensystems)

A[1] := [1,1,1]:

A[2] := [1,1,–1]:

A[3] := [1,–1,1]:

A[4] := [1,–1,–1]:

A[5] := [–1,1,1]:

A[6] := [–1,1,–1]:

A[7] := [–1,–1,1]:

A[8] := [–1,–1,–1]:

A[9] := [phi, 0, Phi]:

A[10] := [–phi, 0, Phi]:

A[11] := [phi, 0, –Phi]:

A[12] := [–phi, 0, –Phi]:

A[13] := [Phi, phi, 0]:

A[14] := [Phi, –phi, 0]:

A[15] := [–Phi, phi, 0]:

A[16] := [–Phi, –phi, 0]:

A[17] := [0, Phi, phi]:

A[18] := [0, Phi, –phi]:

A[19] := [0, –Phi, phi]:

A[20] := [0, –Phi, –phi]:

Die Abbildung 1 gibt die Position mit den Eckennummern im Koordinatensystem. Das Dodekaeder steht auf der Kante A[11] A[12] (kantenständige Darstellung).

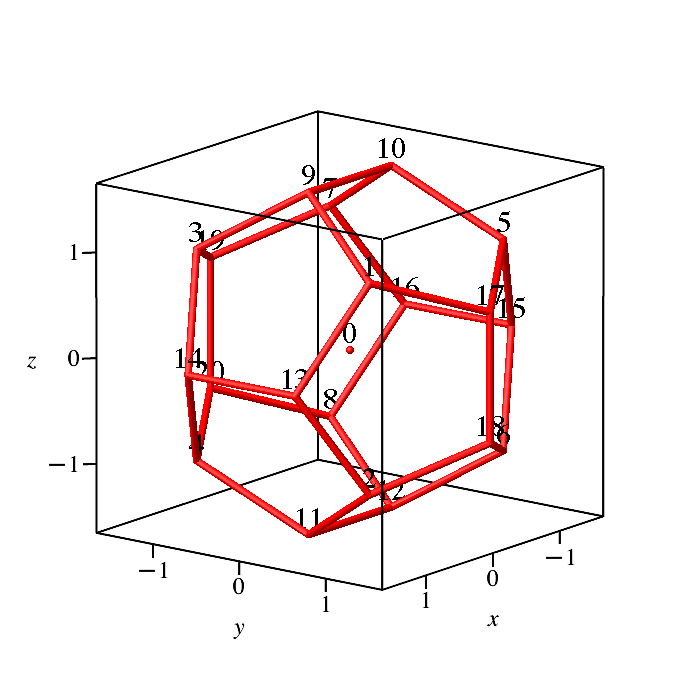
Abb. 1: Position im Koordinatensystem

Die Abbildung 2 zeigt einen Streckenzug den Nummern nach.

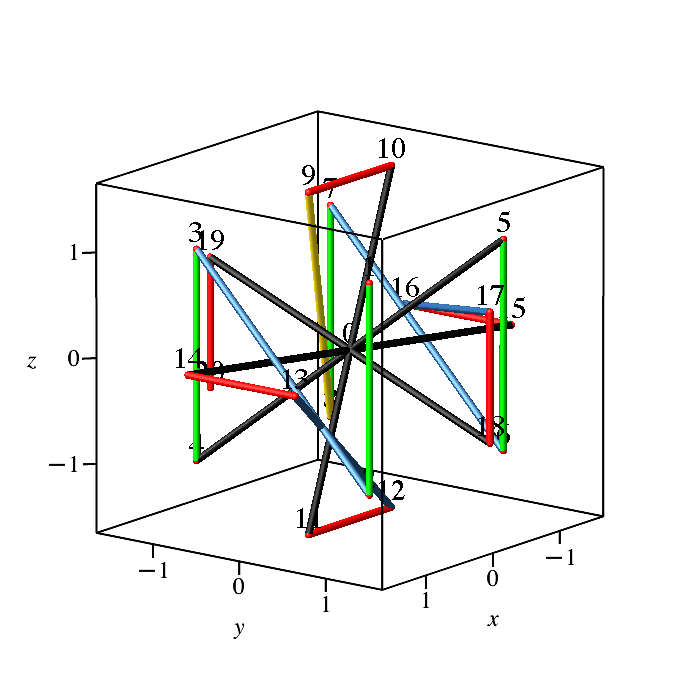
Abb. 2: Streckenzug den Nummern nach

Die Ecken A[1] bis A[8] bilden einen achsenparallelen (Kanten parallel zu den Koordinatenachsen) grünen Würfel (Abb. 3). Es gibt insgesamt fünf Würfel im Dodekaeder, die übrigen vier sind nicht achsenparallel.

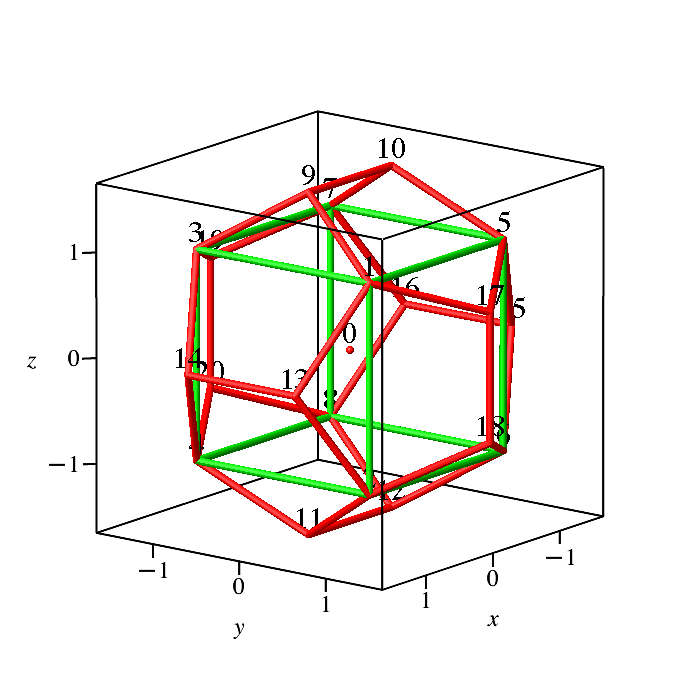
Abb. 3: Würfel im Dodekaeder

Mit den Ecken A[9] bis A[20] lässt sich ein achsenparalleles Rechtecksgerüst bilden (Abb. 4). Die Rechtecke haben das Seitenverhältnis Φ:(1/ Φ) (Langes Goldenes Rechteck). Es gibt insgesamt fünf solche Rechtecksgerüste, die übrigen vier sind nicht achsenparallel.

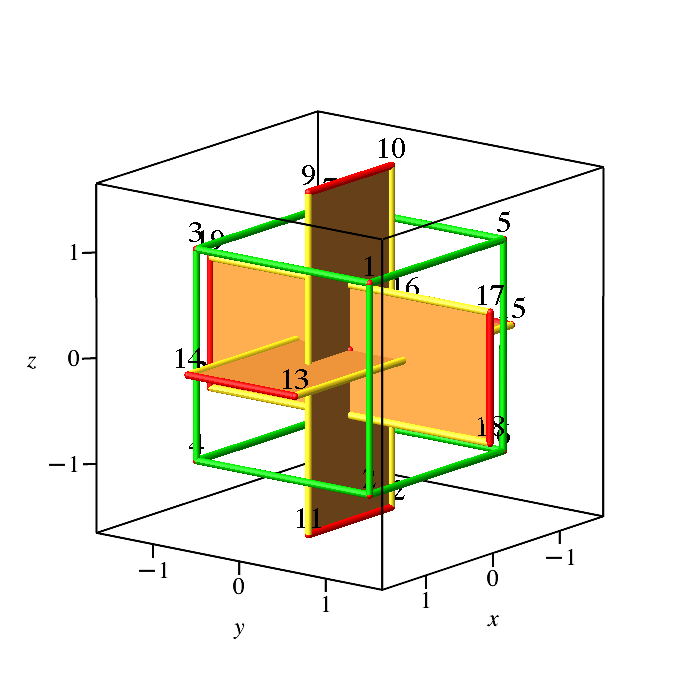
Abb. 4.1: Lange Goldene Rechtecke

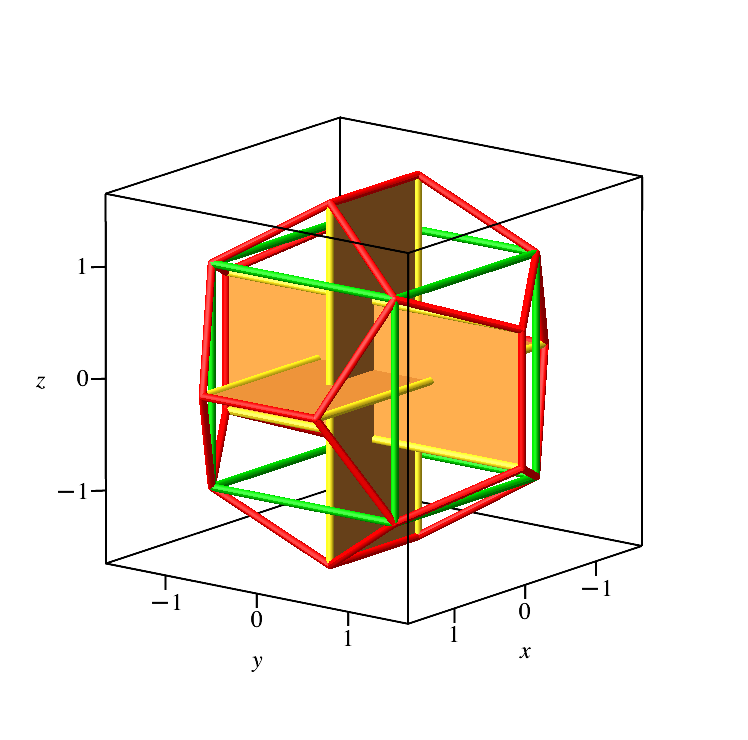
Abb. 4.2: Würfel und Lange Goldene Rechtecke

3 Positionen im Koordinatensystem

Es gibt drei spezielle Positionen im Koordinatensystem: Kantenständig (Abb. 1 und 5.1), eckenständig (Abb. 5.2) und seitenständig (Abb. 5.3).

In der kantenständigen Position (Abb. 5.1) ist die z-Achse eine zweizählige Symmetrieachse.

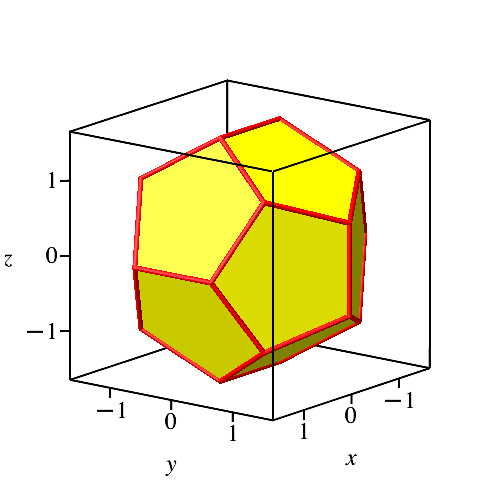
Abb. 5.1: Kantenständig

In der eckenständigen Position (Abb. 5.2) ist die z-Achse eine dreizählige Symmetrieachse.

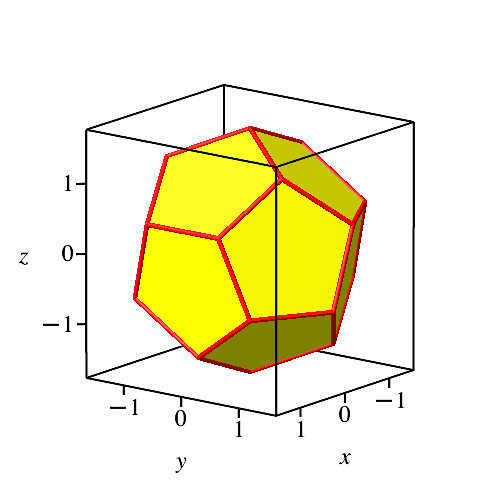
Abb. 5.2: Eckenständig

In der seitenständigen Position (Abb. 5.3) ist die z-Achse eine fünfzählige Symmetrieachse.

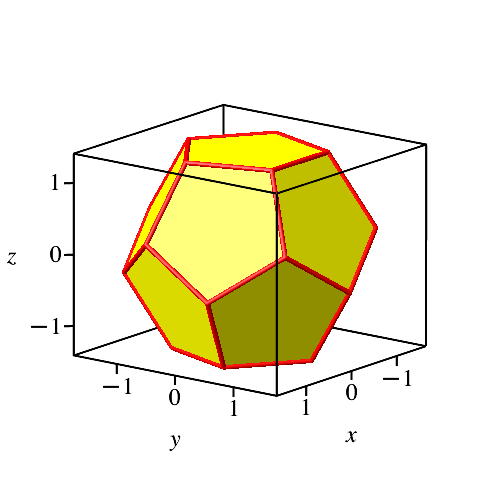
Abb. 5.3: Seitenständig

4 Kanten und Diagonalen

Die Abbildung 6 zeigt das Kantengerüst.

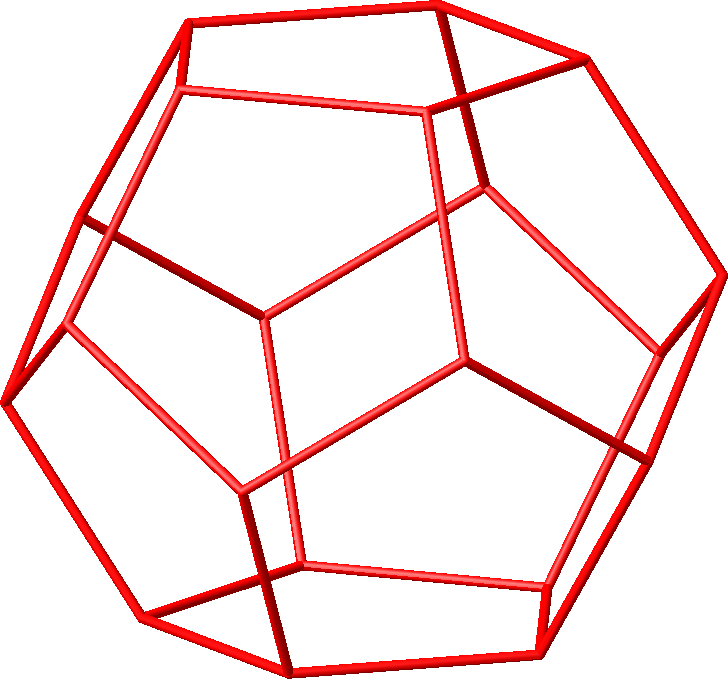
Abb. 6: Kantengerüst

Die Abbildung 7.1 zeigt das Kantengerüst mit sämtlichen Diagonalen.

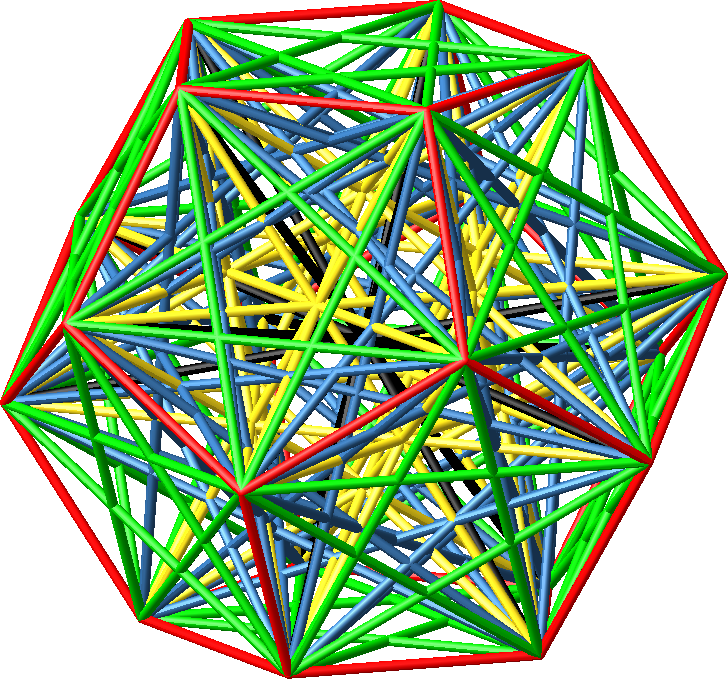
Abb. 7.1: Kantengerüst mit sämtlichen Diagonalen

Die Hamming-Länge einer Diagonale bestimmen wir als die minimale Anzahl von Kanten auf dem Kantengerüst, um vom Anfangspunkt der Diagonale zum Endpunkt zu gelangen. Es handelt sich hier um die sogenannte Hamming-Distanz (Richard Wesley Hamming, 1915-1998). In unserem Kontext ist die Hamming-Länge immer eine natürliche Zahl. Die Kanten selber sind die „Diagonalen“ mit der Hamming-Länge eins. Die längsten Diagonalen (zwischen diametralen Punkten) haben die Hamming-Länge 5.

Die Tabelle 1 gibt eine Übersicht über die Diagonalenlängen. Dabei ist Φ der Goldene Schnitt, Φ ≈ 1.618033988. Die relative euklidische Länge ist bezogen auf die Kantenlänge.

Farbe
Hamming-Länge	1	2	3	4	5
Relative euklidische Länge	1	Φ	Φ √2	1 + Φ	Φ √3
Relative euklidische Länge	1	1.618033988	2.288245610	2.618033986	2.802517076
Anzahl	30	60	60	30	10
Begriff	Kante	Seitenflächendiagonale	Raumdiagonale	Raumdiagonale	Durchmesser

Tab. 1: Diagonalenlängen

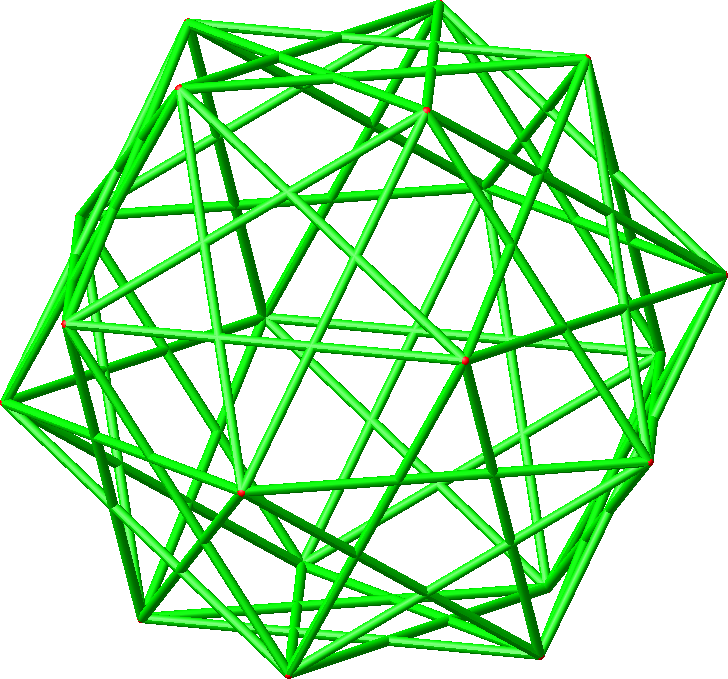
Abb. 7.2: Diagonalen der Hamming-Länge 2

Abb. 7.3: Diagonalen der Hamming-Länge 3

Abb. 7.4: Diagonalen der Hamming-Länge 4

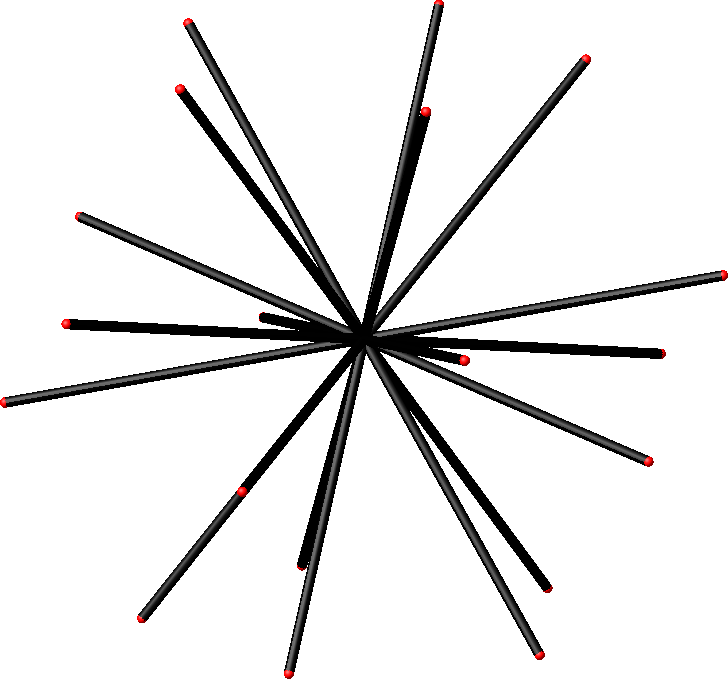
Abb. 7.5: Diagonalen der Hamming-Länge 5

5 Einbau von Flächen

5.1 Dreiecke

5.1.1 Hamming-Seitenlänge 2

Die Abbildung 8.1 zeigt ein Dreieck mit der Hamming-Seitenlänge 2.

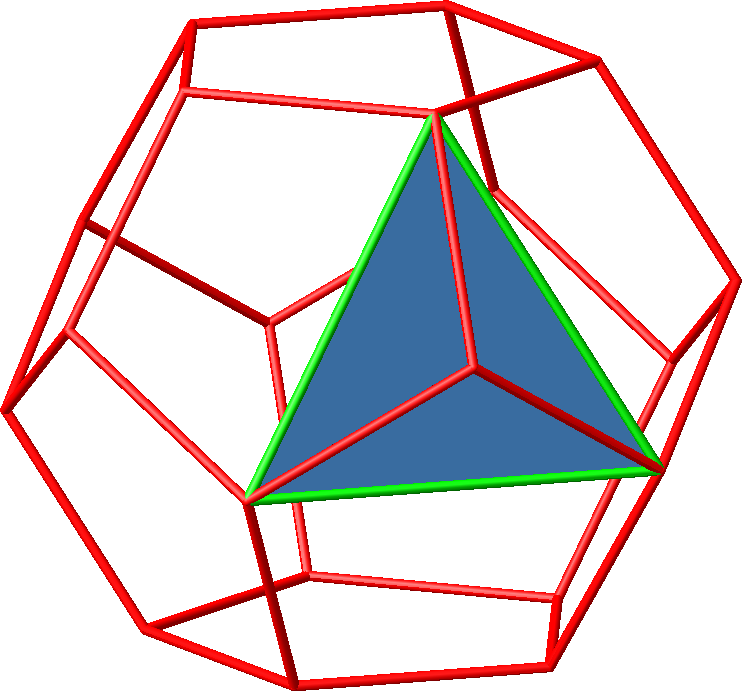
Abb. 8.1: Dreieck mit der Hamming-Seitenlänge 2

In den Abbildungen 8.2 und 8.3 sind alle Dreiecke mit der Hamming-Seitenlänge 2 eingezeichnet. Es gibt 20 solche Dreiecke. Die Figur ist also eine Art Ikosaeder.

Abb. 8.2 Dreiecke der Hamming-Seitenlänge 2

Abb. 8.3 Dreiecke der Hamming-Seitenlänge 2

Abb. 8.4: Dreiecke der Hamming-Seitenlänge 2

5.1.2 Hamming-Seitenlänge 3

Die Abbildung 9.1 zeigt ein einzelnes Dreieck mit der Hamming-Seitenlänge 3.

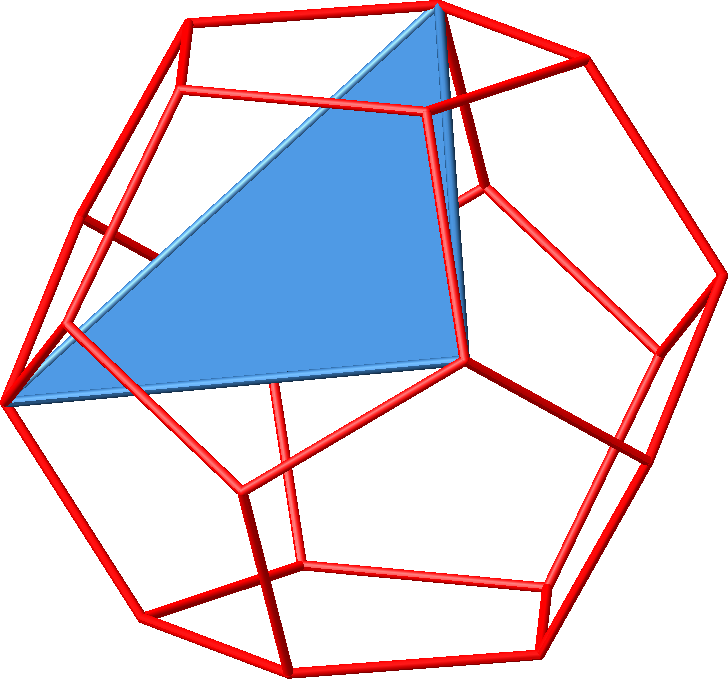
Abb. 9.1: Dreieck mit Hamming-Seitenlänge 3

Je vier Dreiecke bilden ein Tetraeder (Abb. 9.2).

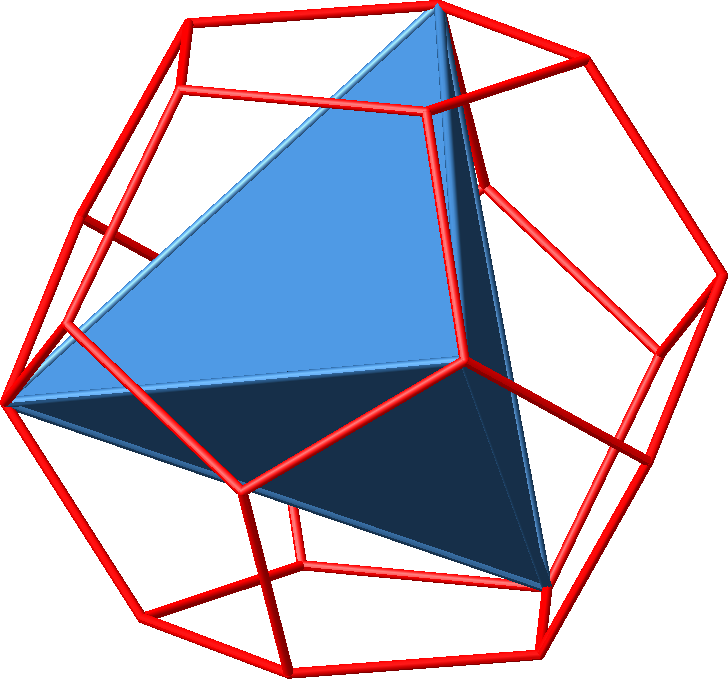
Abb. 9.2: Tetraeder

In den Abbildungen 9.3 und 9.4 sind alle Dreiecke mit der Hamming-Seitenlänge 3 eingezeichnet. Es gibt 40 solche Dreiecke und damit zehn Tetraeder.

Abb. 9.3 Dreiecke und Tetraeder der Hamming-Seitenlänge 3

Abb. 9.4: Dreiecke und Tetraeder der Hamming-Seitenlänge 3

Abb. 9.5: Dreiecke und Tetraeder der Hamming-Seitenlänge 3

5.2 Quadrate

Wir können Quadrate der Hamming-Seitenlänge 2 einbauen.

Die Abbildung 10.1 zeigt ein Einzelquadrat.

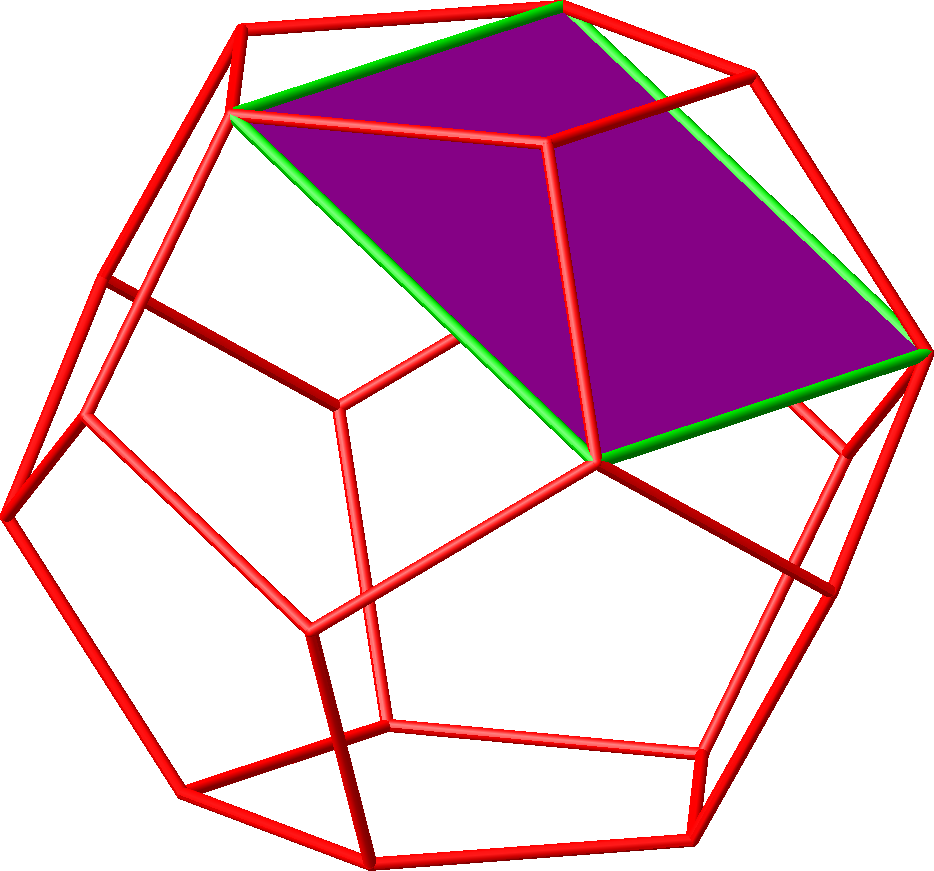
Abb. 10.1: Quadrat

Es gibt 30 Möglichkeiten. Je sechs Quadrate bilden einen Würfel. Die Abbildung 10.2 zeigt einen Würfel. Es gibt 5 Würfel.

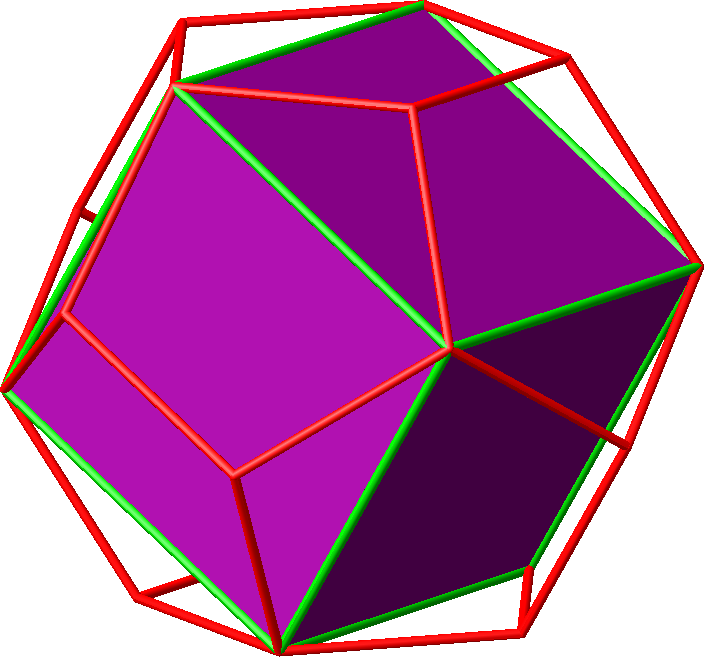
Abb. 10.2: Würfel der Hamming-Seitelänge 2

Die Abbildungen 10.3 und 10.4 zeigen alle Quadrate.

Abb. 10.3: Quadrate

Abb. 10.4: Quadrate

5.3 Fünfecke

5.3.1 Hamming-Seitenlänge 1

Die Abbildung 11.1 zeigt ein Fünfeck der Hamming-Seitenlänge 1. Das ist eine Seitenfläche des Dodekaeders (Abb. 11.2 und 11.3).

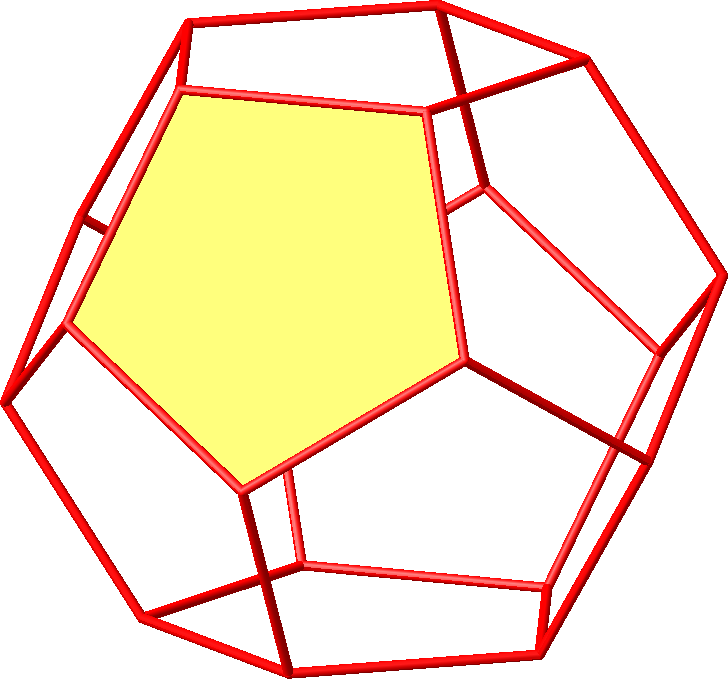
Abb. 11.1: Seitenfläche des Dodekaeders

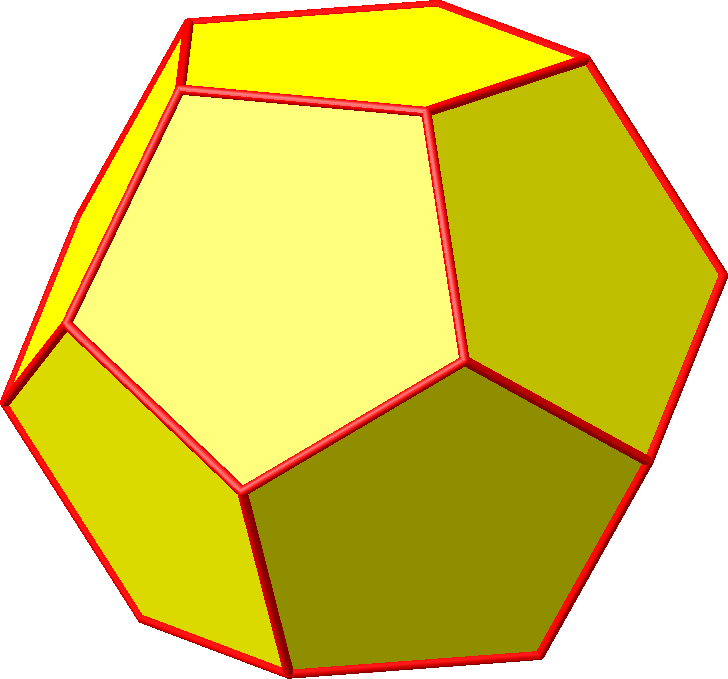
Abb. 11.2: Dodekaeder

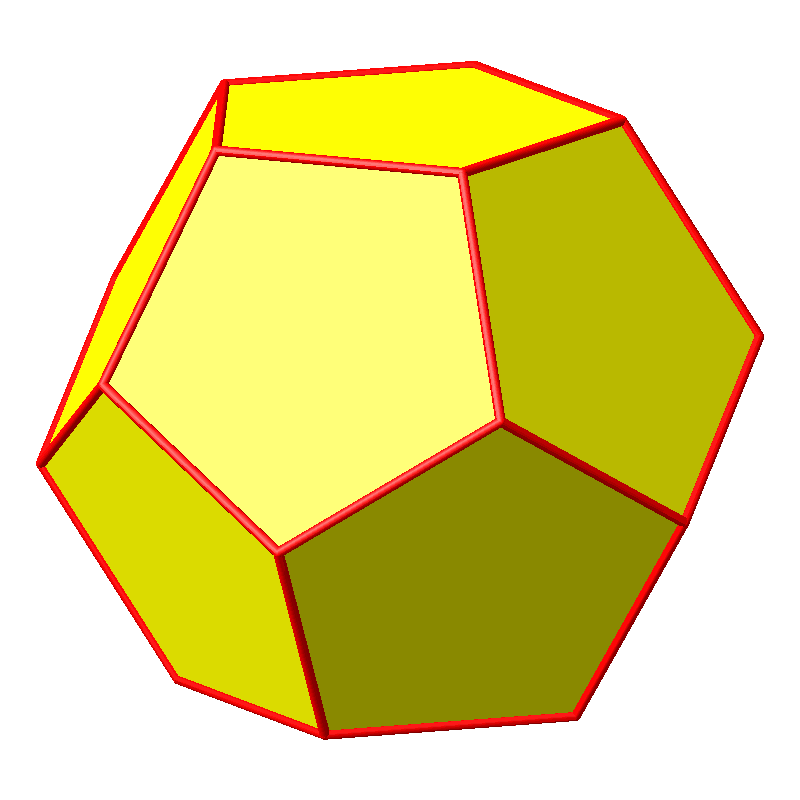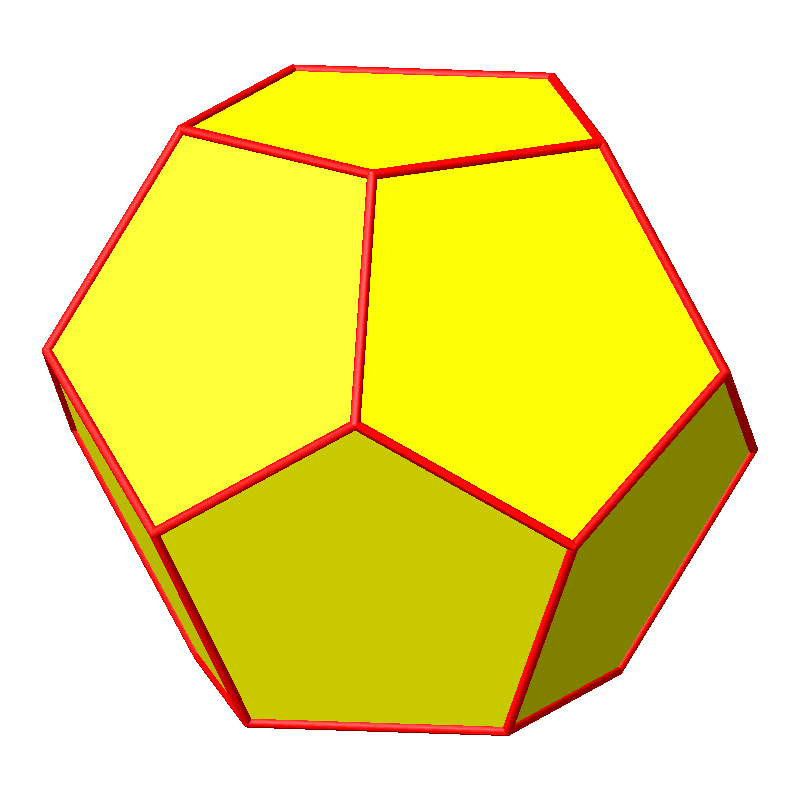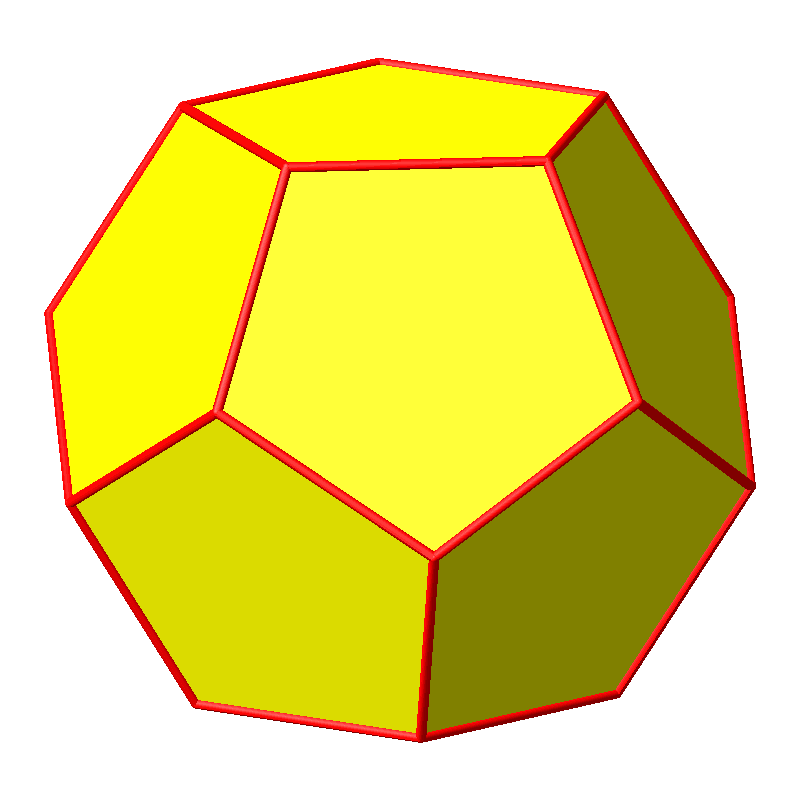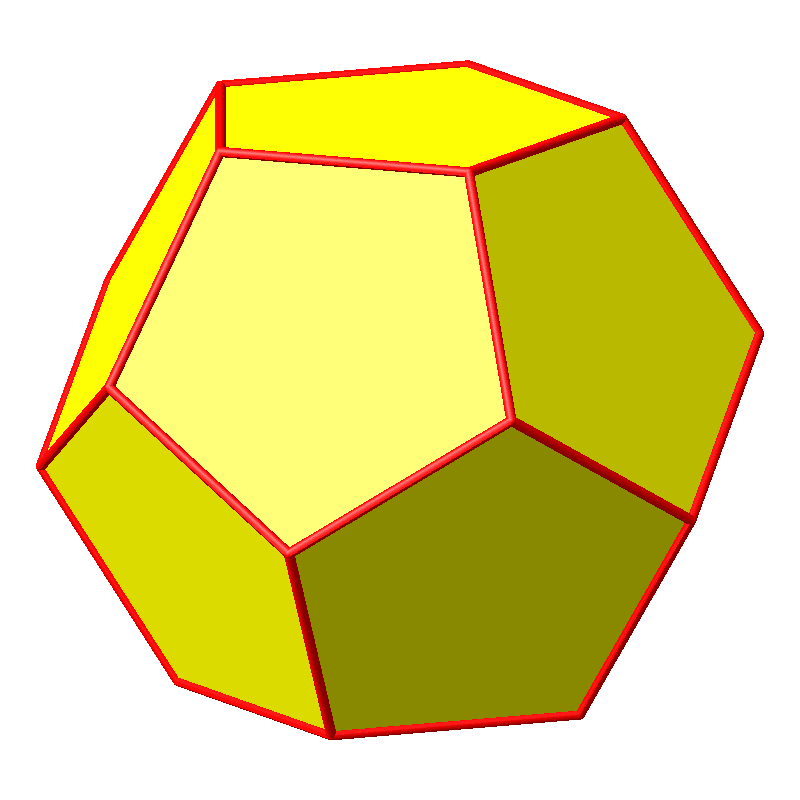
Abb. 11.3: Drehendes Dodekaeder

Abb. 11.4: Drehendes Dodekaeder

5.3.2 Hamming-Seitenlänge 2

Die Abbildung 12.1 zeigt ein einzelnes Fünfeck der Hamming-Seitenlänge 2, die Abbildungen 12.2 und 12.3 alle Fünfecke.

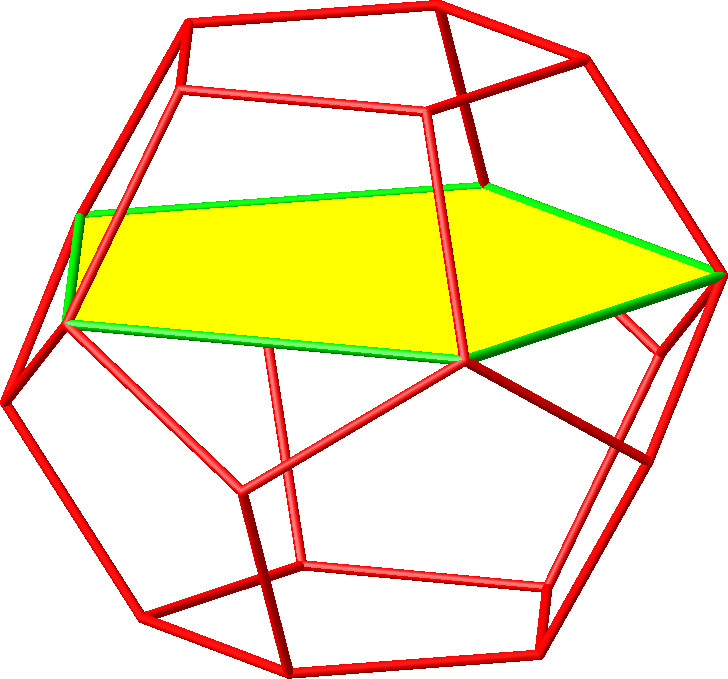
Abb. 12.1: Fünfeck mit Hamming-Seitenlänge 2

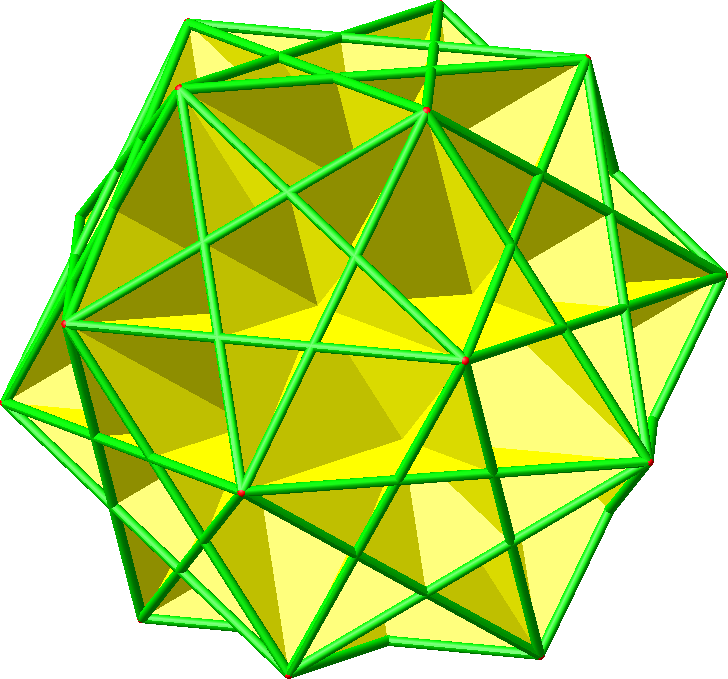
Abb. 12.2: Fünfecke

Abb. 12.3: Fünfecke

5.4 Pentagramme

5.4.1 Hamming-Seitenlänge 2

Die Abbildungen 13.1 bis 13.3 zeigen Pentagramme der Hamming-Seitenlängen 2.

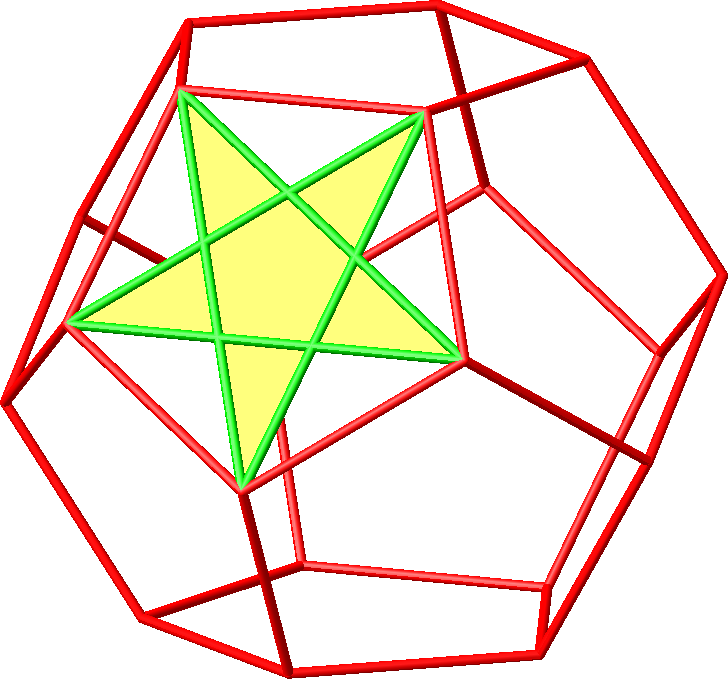
Abb. 13.1: Pentagramm

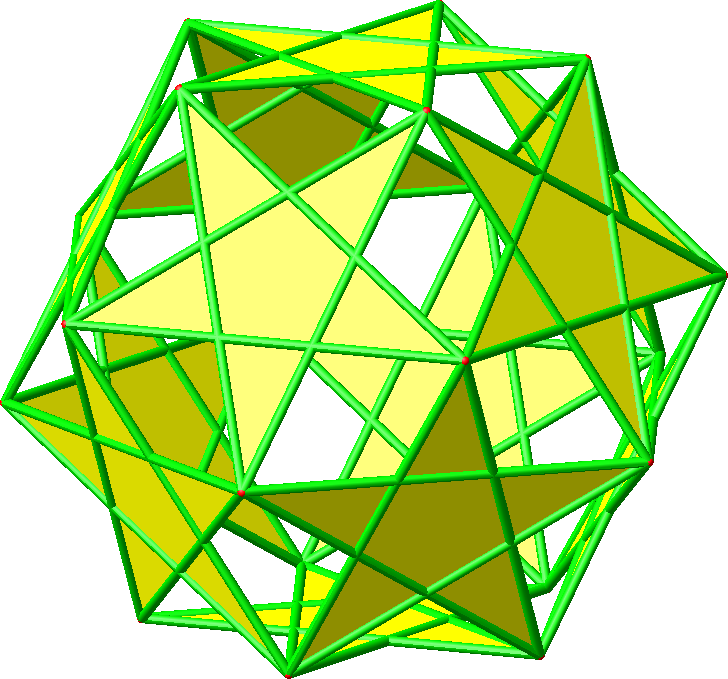
Abb. 13.2: Zwölf Pentagramme

Abb. 13.3: Weihnachten

5.4.2 Hamming-Seitenlänge 4

Die Abbildungen 14.1 bis 14.3 zeigen Pentagramme der Hamming-Seitenlängen 4.

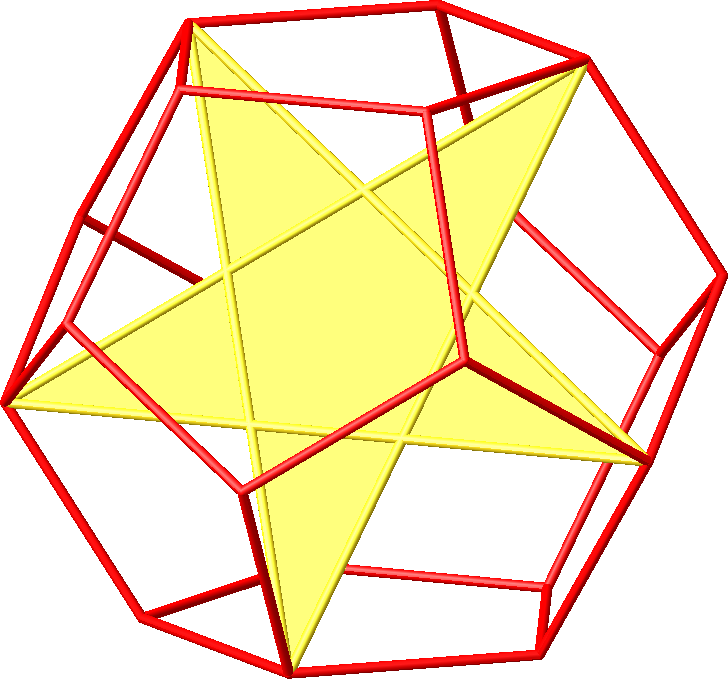
Abb. 14.1: Pentagramm

Der entstehende Stern (Abb. 14.2 und 14.3) heißt Ikosaederstern und ist einer der vier Kepler-Poinsot-Körper. Er enthält im Innern ein regelmäßiges Ikosaeder, daher der Name.

Abb. 14.2: Zwölf Pentagramme

Abb. 14.3: Ikosaederstern

5.5 Rechtecke

5.5.1 Lange Goldene Rechtecke

Ein Langes Goldenes Rechteck hat das Seitenverhältnis Φ:(1/ Φ) = Φ²:1 = (1+ Φ):1. Es entsteht aus dem Goldenen Rechteck durch Ansetzen eines Quadrates auf der Schmalseite (Abb. 15.1). Werden vom Langen Goldenen Rechteck zwei Quadrate abgeschnitten, bleibt ein gewöhnliches Goldenes Rechteck im Hochformat übrig.

Abb. 15.1: Langes Goldenes Rechteck

Die Abbildung 15.2 zeigt ein Langes Goldenes Rechteck im Dodekaeder. Die Hamming-Seitenlängen verhalten sich wie 4:1. Es gibt 15 solche Rechtecke.

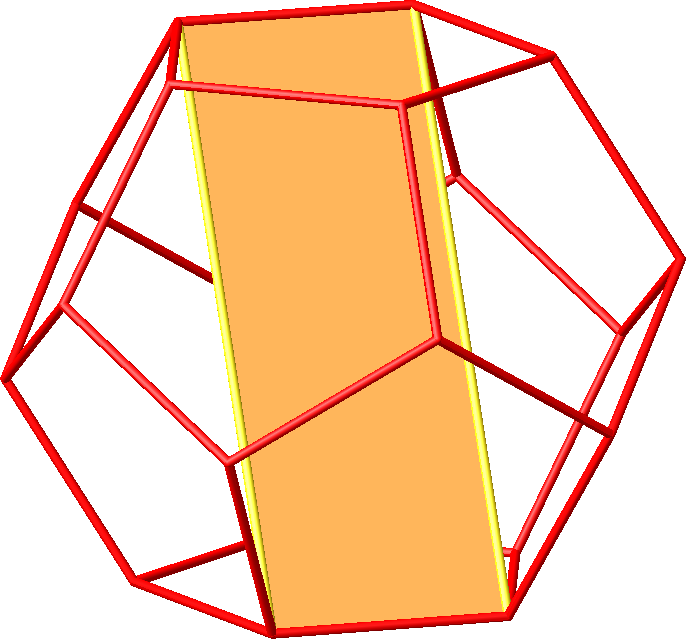
Abb. 15.2: Langes Goldenes Rechteck im Dodekaeder

Die Abbildungen 15.3 und 15.4 zeigen sämtliche Langen Goldenen Rechtecke.

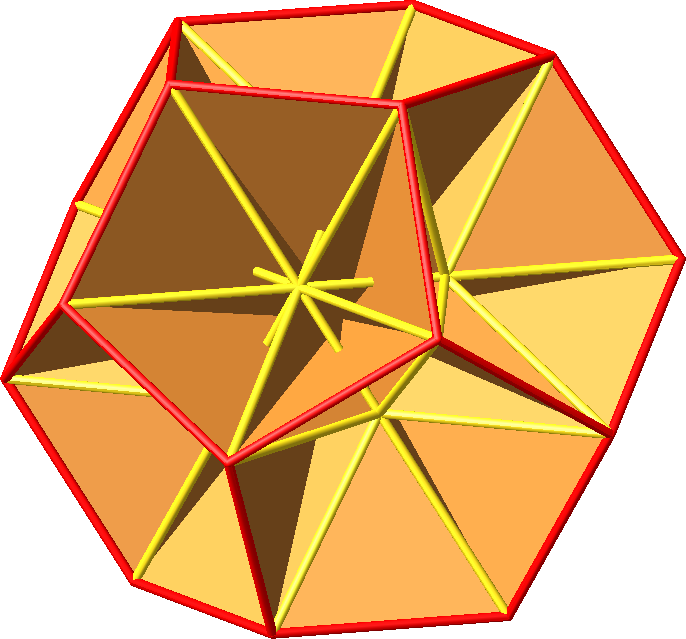
Abb. 15.3: Alle Langen Goldenen Rechtecke

Abb. 15.4: Lange Goldene Rechtecke

5.5.2 DIN-Format

Wir können ein Rechteck im DIN-Format einpassen (Abb. 16.1). Es hat das euklidische Seitenverhältnis √2:1. Die Hamming-Seitenlängen verhalten sich wie 3:2.

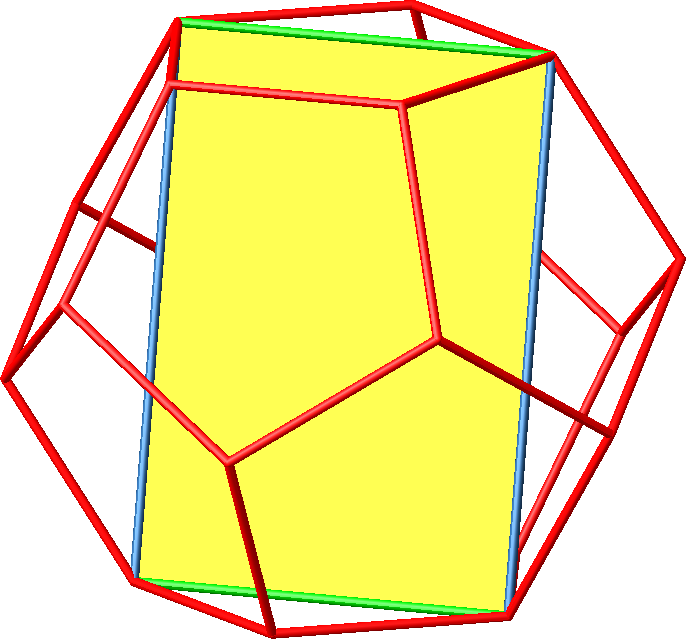
Abb. 16.1: Rechteck im DIN-Format

Es gibt 30 solche Rechtecke (Abb. 16.2 und 16.3).

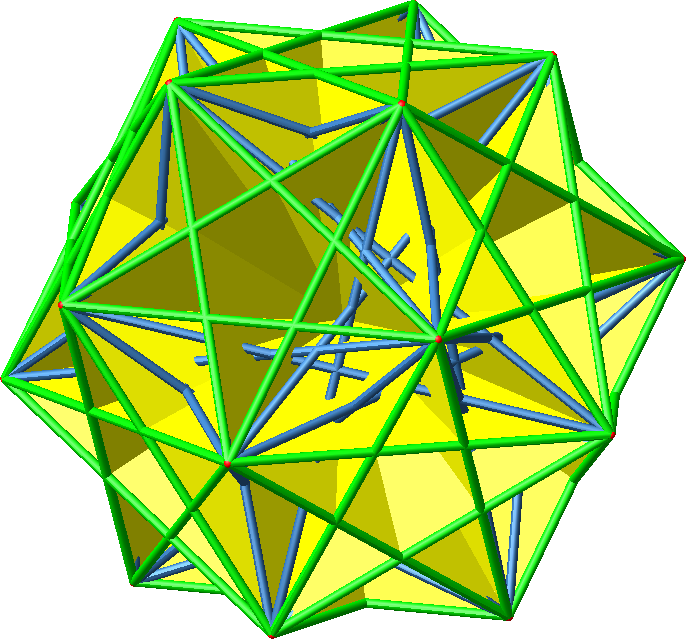
Abb. 16.2: Rechtecke im DIN-Format

Abb. 16.3: Rechtecke im DIN-Format

5.6 Gleichschenklige Dreiecke

Wir unterteilen die im vorhergehenden Abschnitt beschriebenen Rechtecke. Dadurch entstehen vier gleichschenklige Dreiecke, zwei spitze und zwei stumpfe.

Die Spitzen dieser gleichschenkligen Dreiecke liegen im Mittelpunkt des Dodekaeders.

5.6.1 Im Langen Goldenen Rechteck

Abb. 17: Gleichschenklige Dreiecke im Langen Goldenen Rechteck

5.6.1.1 Spitzwinkliges gleichschenkliges Dreieck

Die Abbildung 18.1 zeigt ein solches Dreieck im Dodekaeder.

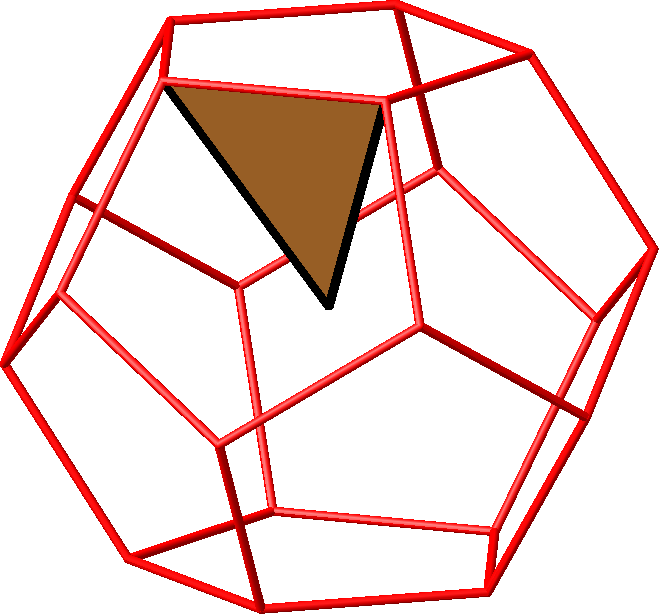
Abb. 18.1 Dreieck im Dodekaeder

Die Abbildungen 18.2 bis 18.4 zeigen alle Dreiecke. Es hat insgesamt 30 Dreiecke, zu jeder Dodekaederkante eines. Wir haben nach innen gerichtete Pyramiden mit der Spitze im Mittelpunkt.

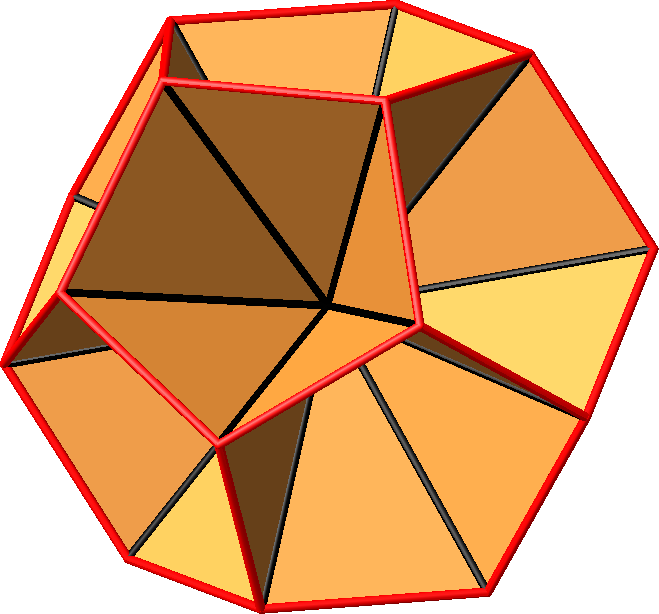
Abb. 18.2: Dreiecke im Dodekaeder

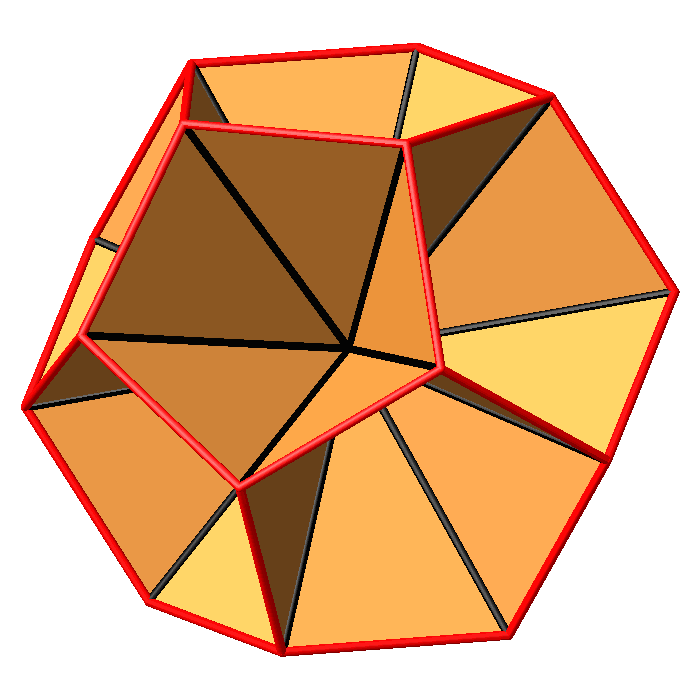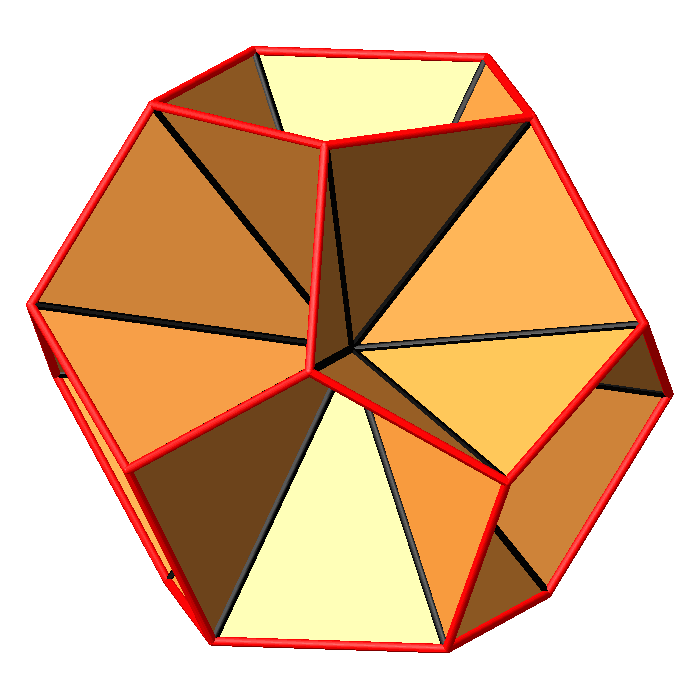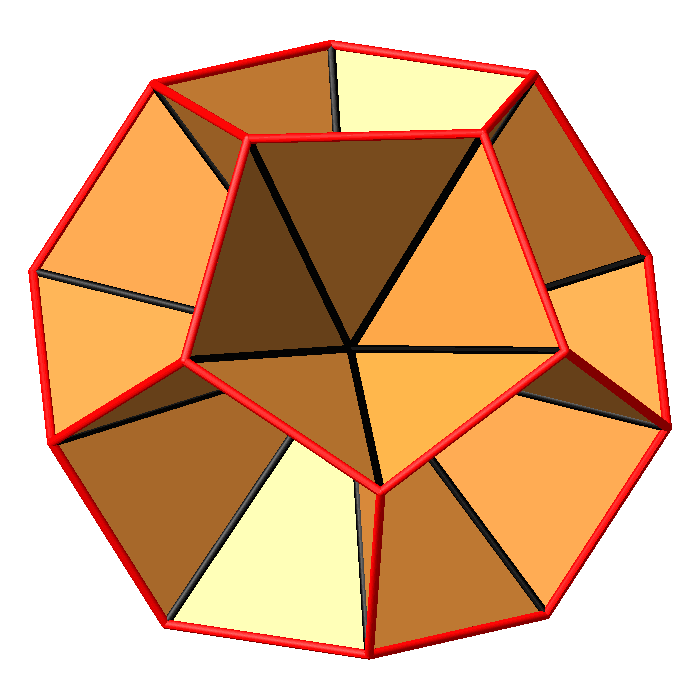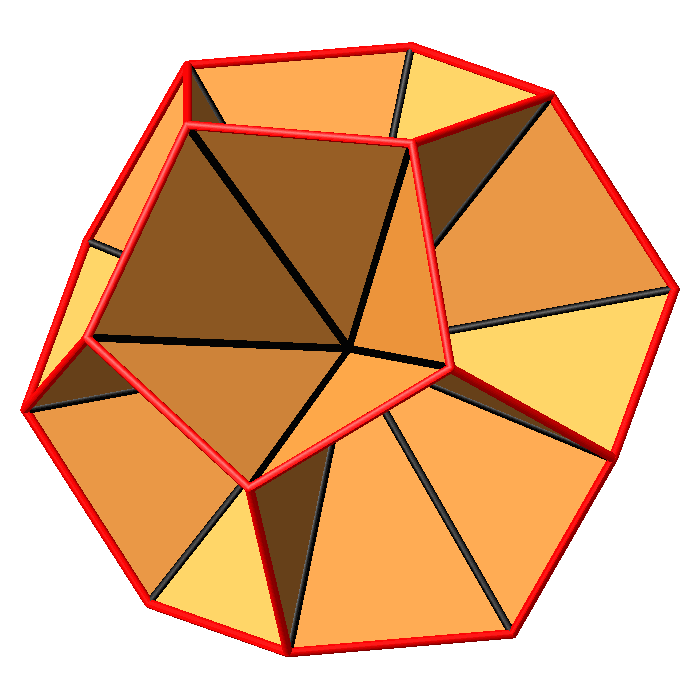
Abb. 18.3: Dreiecke im Dodekaeder

Abb. 18.4: Dreiecke im Dodekaeder

Abb. 18.5: Papiermodell

5.6.1.2 Stumpfwinkliges gleichschenkliges Dreieck

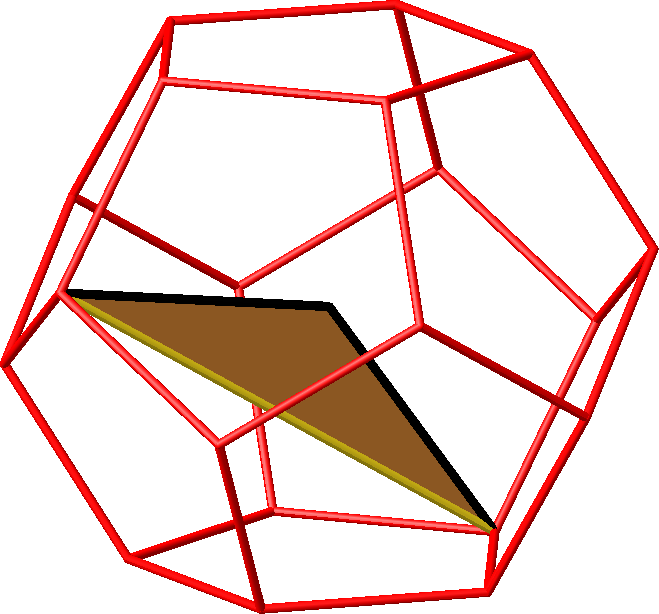
Abb. 19.1: Einzeldreieck

Abb. 19.2: Alle Dreiecke

Abb. 19.3: Alle Dreiecke

Abb. 19.4: Alle Dreiecke

5.6.2 Im DIN-Rechteck

Abb. 20: Gleichschenklige Dreiecke im DIN-Rechteck

5.6.2.1 Spitzwinkliges gleichschenkliges Dreieck

Die Abbildung 21.1 zeigt ein Einzeldreieck. Es gibt insgesamt 60 Dreiecke.

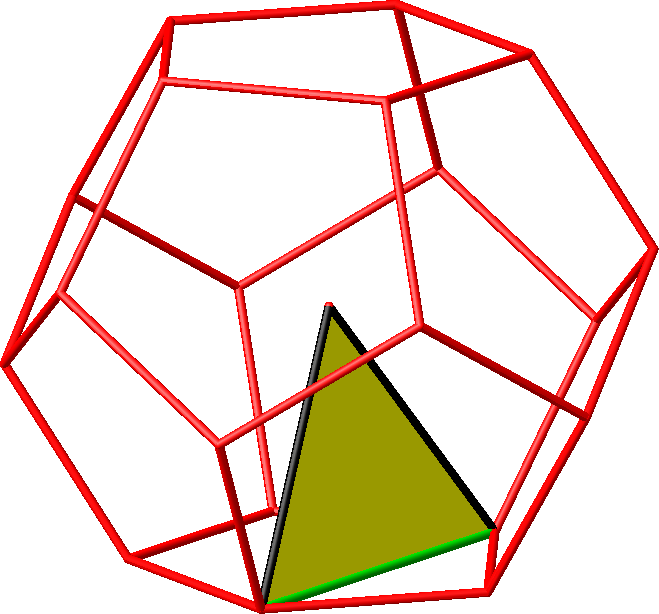
Abb. 21.1: Einzeldreieck im Dodekaeder

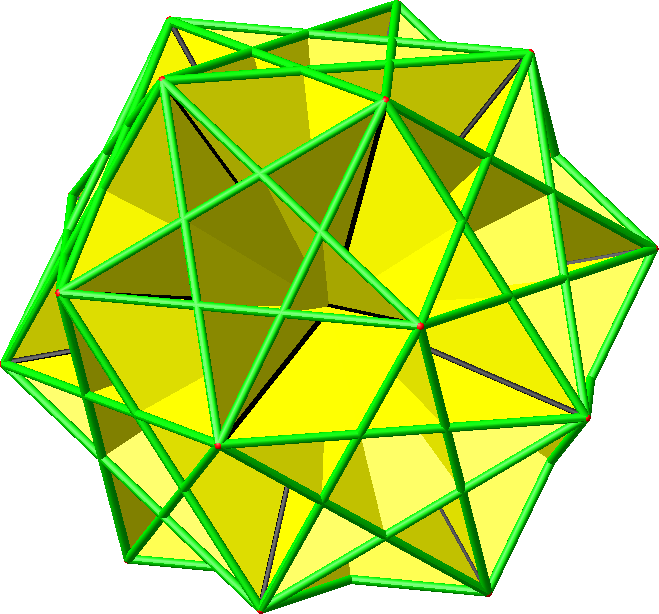
Abb. 21.2: Alle Dreiecke

Abb. 21.3: Alle Dreiecke

Abb. 21.4: Alle Dreiecke

5.6.2.2 Stumpfwinkliges gleichschenkliges Dreieck

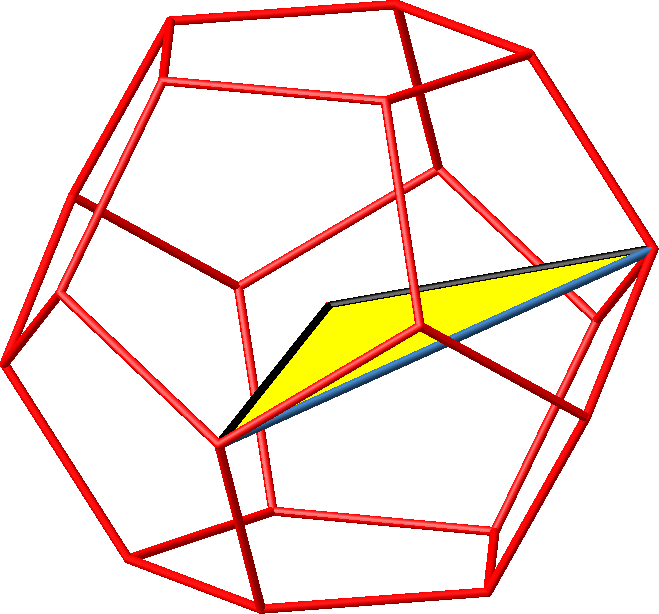
Abb. 22.1:Einzeldreieck

Abb. 22.2: Alle Dreiecke

Abb. 22.3: Alle Dreiecke

Abb. 22.4: Alle Dreiecke