Hans Walser, [20090720a]
Dissection of a convex polygon with central symmetry
1 General case
A polygon with central symmetry has an even number of vertices.
Theorem:
A convex polygon with central symmetry and 2n vertices can be dissected into ![]() parallelograms.
parallelograms.
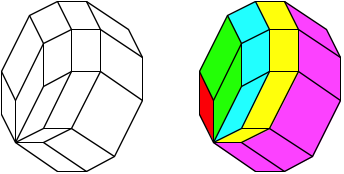
Dissection of a 12-gon
Proof by induction according to the colors [Walser 1983].
We can easily find the dissection by moving copies of the polygon such that every vertex comes once to a particular vertex of the original polygon.
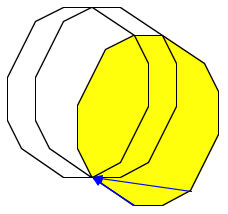
First two steps

Dissection
2 Special cases
2.1 Equilateral polygons
An equilateral polygon with central symmetry can be dissected into rhombi.
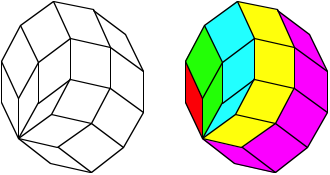
Rhombi
2.2 Regular polygons
We
discuss now regular polygons with 2n
vertices. The dissection we can obtain by moving like above or by rotating the
2n-gon by angles of multiples of ![]() around a particular
vertex ([Lindgren 1972], p. 109, and cover).
around a particular
vertex ([Lindgren 1972], p. 109, and cover).

Dissection of a regular 14-gon
If we are just interested in the vertices of the rhombi, we can work with circles.

Circles will work
2.2.1 n odd
In
this case we get ![]() sets, each
consisting of n congruent rhombi. The
acute angles of the rhombi are
sets, each
consisting of n congruent rhombi. The
acute angles of the rhombi are ![]() .
.
n = 7
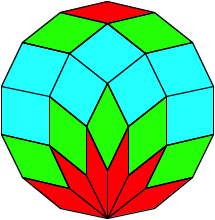
2.2.2 n even
Solution of M. N. DeshpandeŐs Problem 1650 in Mathematics Magazine (2002), p. 227 ([Fischer 2003], with beautiful examples).
We get
![]() sets, each
consisting of n congruent rhombi, and
a set of
sets, each
consisting of n congruent rhombi, and
a set of ![]() squares.
squares.
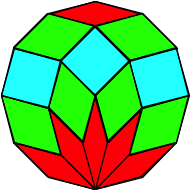
n = 6
References
[Lindgren
1972] Lindgren,
H.: Geometric Dissections. Revised and enlarged by Greg Frederickson. New York:
Dover 1972.
[Walser 1983] Walser, Hans: Ein Zerlegungssatz fźr punktsymmetrische konvexe Vielecke. Elemente der Mathematik (38), 1983, p. 159-160.
Links (2009 / 7 / 20)
[Fischer 2003]
http://www.calpoly.edu/~glfisher/MAA_Dahlia_Paper3.pdf