Hans Walser, [20111226a]
DIN-Format und Pythagoras
Es wird die Idee der pythagoreischen Dreiecke mit dem DIN-Format kombiniert.
1 Einstieg
Ein jedermann im Lande
kennt die Abbildung 1.
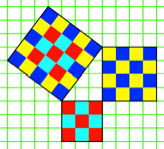
Abb. 1: Pythagoreisches
Dreieck
Die kleinen
ZŠhlquadrate kšnnen durch ZŠhlrechtecke im DIN-Format (also mit dem SeitenverhŠltnis
![]() ) ersetzte werden. Das geht sogar auf zwei Arten (Abb. 2).
) ersetzte werden. Das geht sogar auf zwei Arten (Abb. 2).

Abb. 2: ZŠhlrechtecke
Die beiden
Kathetenrechtecke und das Hypotenusenrechteck haben dann auch das DIN-Format.
Wenn wir die ZŠhlrechtecke abzŠhlen, ist immer noch ![]() , und das rechtwinklige Dreieck hat seine Form nicht
verŠndert. Allerdings passen die Kathetenrechtecke nicht in einen gemeinsamen
Raster. Das liegt daran, dass
, und das rechtwinklige Dreieck hat seine Form nicht
verŠndert. Allerdings passen die Kathetenrechtecke nicht in einen gemeinsamen
Raster. Das liegt daran, dass ![]() eine irrationale
Zahl ist.
eine irrationale
Zahl ist.
Die nahe liegende Idee,
den Quadratraster der Abbildung 1 affin zu verzerren, funktioniert nicht (Abb.
3). Die Kathetenrechtecke liegen nun zwar im selben Raster, aber das
Hypotenusenviereck ist ein Parallelogramm.
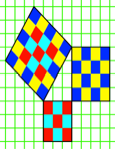
Abb. 3: Affine
Verzerrung
Trotzdem kšnnen wir
quasipythagoreische Dreiecke in einem Rechtecksraster finden.
2
DIN-Raster
Wir arbeiten in einem
Rechtecksraster, dessen Rechtecke das SeitenverhŠltnis ![]() haben. Solche
Raster kšnnen im ăHochformatŇ oder im ăQuerformatŇ vorliegen. In beiden FŠllen
ist es jedoch mšglich, quasipythagoreische rechtwinklige Dreiecke einzupassen
(Abb. 4). Die Ecken der rechtwinkligen Dreiecke sind Rasterpunkte, ebenso die
Ecken der beiden Kathetenrechtecke und des Hypotenusenrechtecks.
haben. Solche
Raster kšnnen im ăHochformatŇ oder im ăQuerformatŇ vorliegen. In beiden FŠllen
ist es jedoch mšglich, quasipythagoreische rechtwinklige Dreiecke einzupassen
(Abb. 4). Die Ecken der rechtwinkligen Dreiecke sind Rasterpunkte, ebenso die
Ecken der beiden Kathetenrechtecke und des Hypotenusenrechtecks.
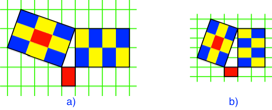
Abb. 4:
Quasipythagoreische rechtwinklige Dreiecke im DIN-Raster
Die beiden Dreiecke
sind kongruent. Der Querformatraster (Abb. 4b) ist aus dem Hochformatraster
(Abb. 4a) durch Halbieren der Rasterrechtecke entstanden. Entsprechend wurden
die beiden Kathetenrechtecke und das Hypotenusenrechteck halbiert.
Die Stimmigkeit der
quasipythagoreischen Figuren lŠsst sich leicht verifizieren. Fźr die Rechnung
wird jeweils die kźrzere Seite der Rasterrechtecke auf 1 normiert.
Im der Abbildung 4a
haben wir: ![]() , also
, also ![]()
Im der Abbildung 4b
ergibt sich: ![]() , also
, also ![]()
In der Abbildung 4a
(Hochformat-Raster) ist die Hypotenuse in ăkleinenŇ Einheiten (kurze Seite der
Rasterrechtecke) gemessen, in der Abbildung 4b (Querformat) in ălangenŇ
Einheiten. Dies ist aber nicht an den Rastertyp gebunden. Die Abbildung 5 zeigt
ein Beispiel im Hochformat, bei dem die Hypotenuse in ălangenŇ Einheiten
gemessen wird.
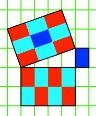
Abb. 5: Hochformat,
Hypotenuse in langen Einheiten
Wir sehen aber sofort,
dass dieses Beispiel durch Vertauschen der beiden Katheten in den Fall der
Abbildung 4b (Querformat) źbergefźhrt werden kann. Dieser wiederum kann durch
Verdoppeln der Rasterrecke in den Fall der Abbildung 4a źbergefźhrt werden. Wir
kšnnen also ohne Verlust an Allgemeinheit eine Standardisierung vornehmen.
3
Standardisierung
Wir arbeiten im
Hochformat-Raster und messen die Hypotenuse in Einheiten der kurzen Rasterrechtecksseite.
Die Abbildung 6 zeigt ein etwas grš§eres Beispiel.
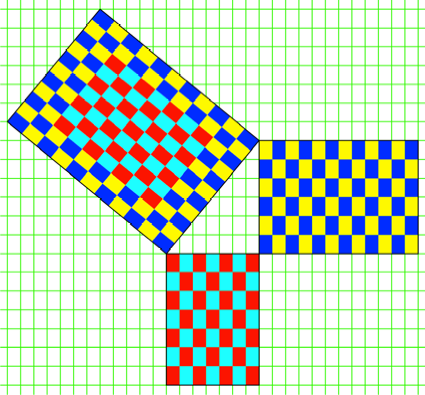
Abb. 6: Grš§eres
Beispiel
Die Stimmigkeit der
Figur lŠsst sich leicht verifizieren:
![]() also
also ![]()
4
Quasipythagoreische Zahlentripel
Wir zŠhlen die
Rasterrechtecke lŠngs der Seiten des rechtwinkligen Dreiecks. Im Beispiel der
Abbildung 4a erhalten wir das Zahlentripel ![]() , im Beispiel der Abbildung 6 das Zahlentripel
, im Beispiel der Abbildung 6 das Zahlentripel ![]() . Die erste Zahl entspricht der horizontalen Kathete im standardisierten
Fall, die zweite Zahl der vertikalen Kathete und die dritte Zahl der Hypotenuse.
Die Zahlentripel
. Die erste Zahl entspricht der horizontalen Kathete im standardisierten
Fall, die zweite Zahl der vertikalen Kathete und die dritte Zahl der Hypotenuse.
Die Zahlentripel ![]() der beiden Beispiele
genźgen der Gleichung:
der beiden Beispiele
genźgen der Gleichung:
![]()
Wegen der RasterlŠnge ![]() in vertikaler
Richtung ist diese Bedingung allgemein genau dann erfźllt, wenn wir eine
quasipythagoreische Figur in standardisierter Form haben.
in vertikaler
Richtung ist diese Bedingung allgemein genau dann erfźllt, wenn wir eine
quasipythagoreische Figur in standardisierter Form haben.
Diese
quasipythagoreischen Zahlentripel kšnnen in Anlehnung an die gewšhnlichen
pythagoreischen Zahlentripel zum Beispiel wie folgt generiert werden. Es zeigt
sich allerdings, dass dazu zwei verschiedene FormelsŠtze benštigt werden.
4.1
Erste Parametrisierung
Wir wŠhlen zwei
teilerfremde Parameter u mit u ungerade und ![]() . Dann erfźllen die Zahlen
. Dann erfźllen die Zahlen
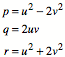
die Bedingung ![]() , wie man leicht nachrechnet. Zudem ist das Tripel teilerfremd.
Die Tabelle 1 zeigt die ersten Beispiele.
, wie man leicht nachrechnet. Zudem ist das Tripel teilerfremd.
Die Tabelle 1 zeigt die ersten Beispiele.
|
u |
v |
p |
q |
r |
|
3 |
1 |
7 |
6 |
11 |
|
3 |
2 |
1 |
12 |
17 |
|
5 |
1 |
23 |
10 |
27 |
|
5 |
2 |
17 |
20 |
33 |
|
5 |
3 |
7 |
30 |
43 |
|
7 |
1 |
47 |
14 |
51 |
|
7 |
2 |
41 |
28 |
57 |
|
7 |
3 |
31 |
42 |
67 |
|
7 |
4 |
17 |
56 |
81 |
|
9 |
1 |
79 |
18 |
83 |
|
9 |
2 |
73 |
36 |
89 |
|
9 |
4 |
49 |
72 |
113 |
|
9 |
5 |
31 |
90 |
131 |
|
11 |
1 |
119 |
22 |
123 |
|
11 |
2 |
113 |
44 |
129 |
|
11 |
3 |
103 |
66 |
139 |
|
11 |
4 |
89 |
88 |
153 |
|
11 |
5 |
71 |
110 |
171 |
|
11 |
6 |
49 |
132 |
193 |
|
11 |
7 |
23 |
154 |
219 |
|
13 |
1 |
167 |
26 |
171 |
|
13 |
2 |
161 |
52 |
177 |
|
13 |
3 |
151 |
78 |
187 |
|
13 |
4 |
137 |
104 |
201 |
|
13 |
5 |
119 |
130 |
219 |
|
13 |
6 |
97 |
156 |
241 |
|
13 |
7 |
71 |
182 |
267 |
|
13 |
8 |
41 |
208 |
297 |
|
13 |
9 |
7 |
234 |
331 |
Tabelle 1
Fźr ![]() und
und ![]() ergibt sich das
Tripel
ergibt sich das
Tripel ![]() der Abbildung 6.
der Abbildung 6.
Schšn und gut.
Allerdings fehlt das Beispiel der Abbildung 4a). Dort haben wir das Tripel ![]() . Dazu wźrden die Parameter
. Dazu wźrden die Parameter ![]() und
und ![]() gehšren. Wir
mźssen also einen zweiten Anlauf nehmen.
gehšren. Wir
mźssen also einen zweiten Anlauf nehmen.
4.2
Zweite Parametrisierung
Wir wŠhlen zwei
teilerfremde Parameter u und v mit ![]() und v ungerade. Dann erfźllen die Zahlen
und v ungerade. Dann erfźllen die Zahlen
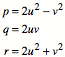
die Bedingung ![]() , wie man leicht nachrechnet. Zudem ist das Tripel teilerfremd.
Die Tabelle 2 zeigt die ersten Beispiele.
, wie man leicht nachrechnet. Zudem ist das Tripel teilerfremd.
Die Tabelle 2 zeigt die ersten Beispiele.
|
u |
v |
p |
q |
r |
|
1 |
1 |
1 |
2 |
3 |
|
2 |
1 |
7 |
4 |
9 |
|
3 |
1 |
17 |
6 |
19 |
|
4 |
1 |
31 |
8 |
33 |
|
4 |
3 |
23 |
24 |
41 |
|
4 |
5 |
7 |
40 |
57 |
|
5 |
1 |
49 |
10 |
51 |
|
5 |
3 |
41 |
30 |
59 |
|
5 |
7 |
1 |
70 |
99 |
|
6 |
1 |
71 |
12 |
73 |
|
6 |
5 |
47 |
60 |
97 |
|
6 |
7 |
23 |
84 |
121 |
|
7 |
1 |
97 |
14 |
99 |
|
7 |
3 |
89 |
42 |
107 |
|
7 |
5 |
73 |
70 |
123 |
|
7 |
9 |
17 |
126 |
179 |
|
8 |
1 |
127 |
16 |
129 |
|
8 |
3 |
119 |
48 |
137 |
|
8 |
5 |
103 |
80 |
153 |
|
8 |
7 |
79 |
112 |
177 |
|
8 |
9 |
47 |
144 |
209 |
|
8 |
11 |
7 |
176 |
249 |
|
9 |
1 |
161 |
18 |
163 |
|
9 |
5 |
137 |
90 |
187 |
|
9 |
7 |
113 |
126 |
211 |
|
9 |
11 |
41 |
198 |
283 |
|
10 |
1 |
199 |
20 |
201 |
|
10 |
3 |
191 |
60 |
209 |
|
10 |
7 |
151 |
140 |
249 |
|
10 |
9 |
119 |
180 |
281 |
|
10 |
11 |
79 |
220 |
321 |
|
10 |
13 |
31 |
260 |
369 |
Tabelle 2
Hier sehen wir nun
zuoberst das Beispiel der Abbildung 4a.
Die Abbildung 7 zeigt
den Fall ![]() ,
, ![]() mit dem Tripel
mit dem Tripel ![]() .
.
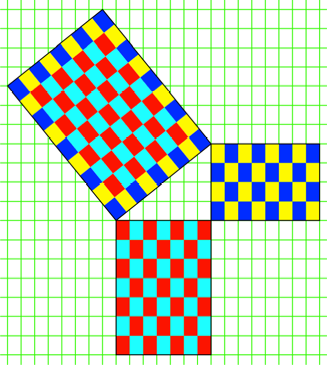
Abb. 7: Tripel (7, 4, 9)
Ich wei§ nicht, ob die
Vereinigung der beiden Tabellen (ad infinitum gedacht) nun alle FŠlle umfasst.
In interessantes zahlentheoretisches Problem.
5
Das Kantholz im Nacken
ăDas Kantholz im
NackenŇ war frźher ein didaktisches Prinzip. Das Kantholz war das Lineal des
Lehrers, es hatte einen quadratischen Querschnitt (damit man durch ăAbrollenŇ
eine Lineatur ziehen konnte). Ein Quader der LŠnge p mit quadratischem Querschnitt der SeitenlŠnge q hat die DiagonalenlŠnge r mit ![]() . Wir sind also beim Thema.
. Wir sind also beim Thema.
Das Kantholz hat als
Motivationsprinzip ausgedient. PISA sei Dank.
6
†berlagerung von DIN-Rastern
6.1
Beispiele mit der ersten Parametrisierung
Wir zeichnen in der
Abbildung 6 das ursprźngliche Rechtecksraster vor die quasipythagoreische Figur
(Abb. 8). Wir haben somit im Bereich des Hypotenusenrechtecks eine †berlagerung
von zwei kongruenten Rastern. Wir stellen fest, dass au§er den Eckpunkten des
Hypotenusenrechteckes noch weitere Punkte den beiden Rastern gemeinsam sind.
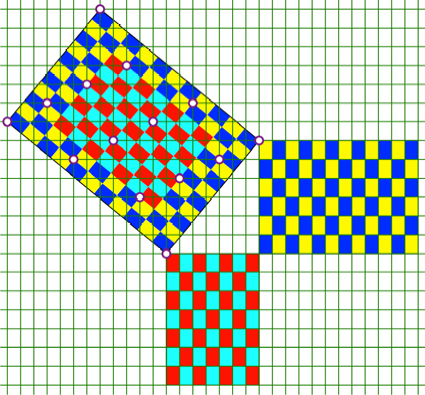
Abb. 8: †berlagerung von
Rastern. Gemeinsame Punkte
Wir kšnnen diese beiden
Rastern gemeinsamen Punkte zu einem neuen Rechtecksraster im DIN-Format
erweitern (Abb. 9).
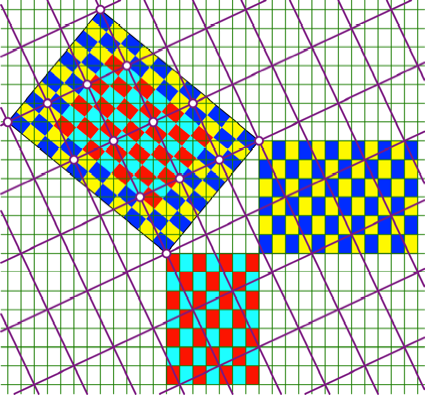
Abb. 9: †berlagerungsraster
fźr u = 3, v = 1
Feststellungen ohne
Beweis:
Der ursprźngliche
Raster und der Raster des Hypotenusenrechteckes sind gegenźber diesem neuen
Raster gespiegelt.
Die Rasterlinien des
†berlagerungsrasters durch die Dreiecksecke links unten sind die innere und
Šu§ere Winkelhalbierende des dortigen Dreieckswinkels.
Die kurzen
Rechtecksseiten des †berlagerungsrasters haben die LŠnge ![]() .
.
Die zugehšrigen
Rasterlinien haben im Basisraster ein Steigungsdreieck mit Horizontalweite u und der Vertikalweite v. Die Steigung ist im Basisraster ![]() , geometrisch also
, geometrisch also ![]() .
.
6.2
Beispiele mit der zweiten Parametrisierung
Nehmen wir das
einfachste Beispiel mit ![]() und
und ![]() , das zum Tripel
, das zum Tripel ![]() fźhrt (Abb. 7).
Wir erhalten wieder einen †berlagerungsraster (Abb. 10).
fźhrt (Abb. 7).
Wir erhalten wieder einen †berlagerungsraster (Abb. 10).
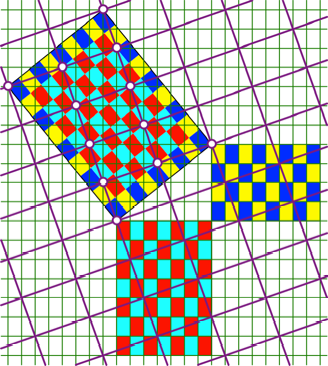
Abb. 10: †berlagerungsraster
fźr u = 2, v = 1
Feststellungen ohne
Beweis:
Der ursprźngliche
Raster und der Raster des Hypotenusenrechteckes sind gegenźber diesem neuen
Raster gespiegelt.
Die Rasterlinien des
†berlagerungsrasters durch die Dreiecksecke links unten sind die innere und
Šu§ere Winkelhalbierende des dortigen Dreieckswinkels.
Die kurzen
Rechtecksseiten des †berlagerungsrasters haben die LŠnge ![]() .
.
Die zugehšrigen
Rasterlinien haben im Basisraster ein Steigungsdreieck mit Horizontalweite v und der Vertikalweite –u. Die Steigung ist im Basisraster ![]() , geometrisch also
, geometrisch also ![]() . Das ist der einzige Unterschied zur ersten
Parametrisierung.
. Das ist der einzige Unterschied zur ersten
Parametrisierung.
7
Komplexe Zahlen
Wir kšnnen die
Parametrisierungen auch mit komplexen Zahlen beschreiben.
7.1
Erste Parametrisierung
Wir wŠhlen ![]() . Damit wird:
. Damit wird:
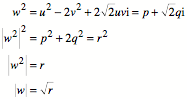
7.2
Zweite Parametrisierung
Wir wŠhlen ![]() . Damit wird:
. Damit wird:
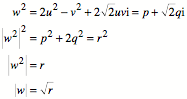
8
Ausblick
Statt mit
DIN-Rechtecken mit dem SeitenverhŠltnis ![]() kšnnen wir mit
Rechtecken im SeitenverhŠltnis
kšnnen wir mit
Rechtecken im SeitenverhŠltnis ![]() , arbeiten. Die Abbildung 11 zeigt ein Beispiel mit Rechtecken
im SeitenverhŠltnis
, arbeiten. Die Abbildung 11 zeigt ein Beispiel mit Rechtecken
im SeitenverhŠltnis ![]() .
.
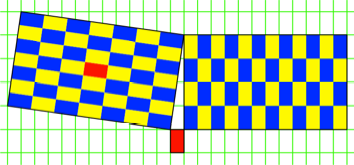
Abb. 11:
SeitenverhŠltnis ![]()
Der Rechtecksraster
lŠsst sich in einen Dreiecksraster umbauen (Abb. 12).
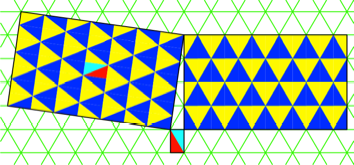
Abb. 12: Dreiecksraster