Hans Walser, [20120217]

Crossvektoren und Fibonacci

Iteration des Vektorprodukts (Crossprodukts). Beispiele

1 Crossvektoren

Wir arbeiten mit den Einheitsvektoren:

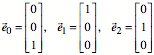
Es sei , und weiter (Reihenfolge beachten). Welche Folge entsteht?

Bearbeitung

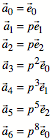
Allgemein ist:

Dabei ist die n-te Fibonacci-Zahl. Beweis induktiv.

2 Crossvektoren

Wir arbeiten mit den Einheitsvektoren:

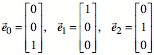
Es sei , und weiter (Reihenfolge beachten). Welche Folge entsteht?

Bearbeitung

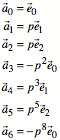
Allgemein ist:

Dabei ist die n-te Fibonacci-Zahl. Beweis induktiv.

3 Crossvektoren

Wir arbeiten mit den Einheitsvektoren:

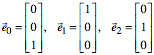
Es sei , und weiter (Reihenfolge beachten).

Bearbeitung

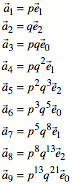
Allgemein ist:

Dabei ist die n-te Fibonacci-Zahl.

Beweis induktiv.

4 Crossvektoren

Mit den Startvektoren und verwenden wir die Rekursion:

Was geschieht?

Bearbeitung

Zunächst ist:

Somit bilden die drei Vektoren ein rechtshändiges Orthogonalsystem.

Explizit ist:

Für die Längen gilt:

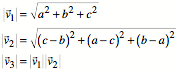
Weiter ist:

Daher ist .

Weiter ist:

Also .

Weiter ist:

Also .

Weiter ist:

Es entstehen die Fibonacci-Zahlen:

Für die Koeffizienten erhalten wir:

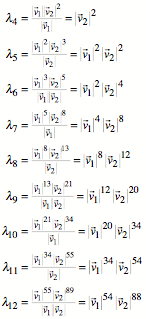
Wir müssen auf gerade Fibonacci-Zahlen abrunden: