1 Three collinear points

Let a, b be parallel lines, and c a circle between a and b touching a in A (Fig. 1a), and d a circle between a and b touching b in B and c in C (Fig. 1b).

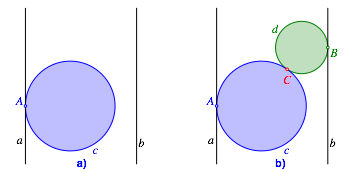
Fig. 1: Circles between two parallel lines

The three points A, B, C are collinear (Fig. 2a).

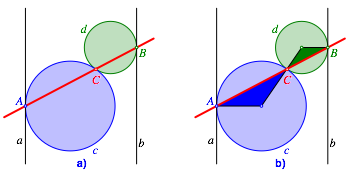
Fig. 2: Collinear points. Proof without words

The figure 2b gives a proof without words.

2 Reflection about a circle

We reflect the figure 2a about an arbitrary circle (purple in Fig. 3).

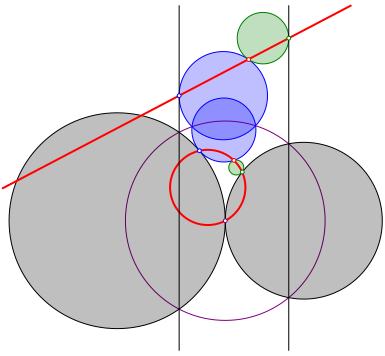
Fig. 3: Reflection about a circle

Thus we get a sequence of touching circles. The touching points are cocyclic (Fig. 4).

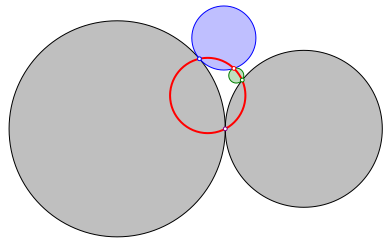
Fig. 4: Cocyclic points