Hans Walser, [20160604]
Chordalkreis
1 Worum geht es?
Verallgemeinerung der Chordale (Potenzgerade). Ebenfalls Verallgemeinerung des Kreises des Apollonius.
2 Potenz
Die Potenz p(P, k(M, r)) eines Punktes P bezźglich eines Kreises k(M, r) mit Mittelpunkt M und Radius r ist gegeben durch:
![]() (1)
(1)
Es gilt der Satz:
Sind X und Y die Schnittpunkte einer beliebigen Geraden g durch P mit dem Kreis k, so ist:
![]() (2)
(2)
Fźr Punkte P au§erhalb des Kreises k ist die Potenz positiv. Sie ist gleich dem Quadrat der LŠnge eines Tangentenabschnittes von P nach k.
Fźr Punkte P auf dem Kreis k ist die Potenz null.
Fźr Punkte P innerhalb des Kreises k ist die Potenz negativ.
3 PotenzverhŠltnis
Gegeben seien nun zwei Kreise k1(M1(x1, y1), r1) und k2(M2(x2, y2), r2) und ein VerhŠltnis v. Wir fragen nach der Menge der Punkte P(x,y) mit der Eigenschaft:
![]() (3)
(3)
In Koordinaten erhalten wir:
![]() (4)
(4)
Die Gleichung (4) ist im allgemeinen Fall eine Kreisgleichung.
Fźr v = 1 ist (4) nur noch linear, also eine Geradengleichung.
4 Chordalkreis und Chordale
Im allgemeinen Fall beschreibt (4) einen Kreis, den Chordalkreis.
Fźr v = 1 beschreibt (4) eine Gerade, die Chordale oder Potenzgerade.
In den Beispielen der Abbildung sind jeweils ein Chordalkreis rot fźr v = ½, die Chordale grźn (fźr v = 1) und ein Chordalkreis blau fźr v = 5 eingezeichnet. Die beiden gegebenen Kreise k1 und k2 sowie deren Mittelpunkte sind schwarz.
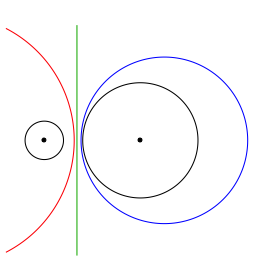
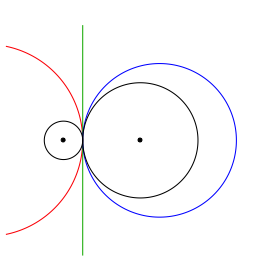
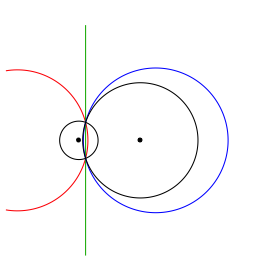
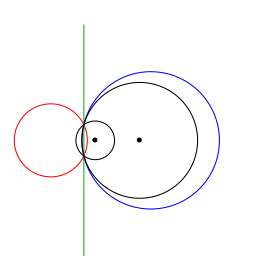
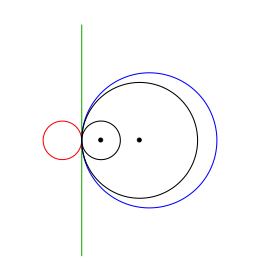
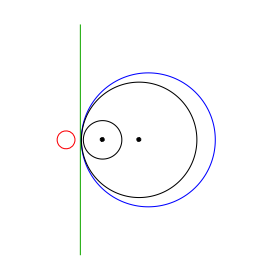
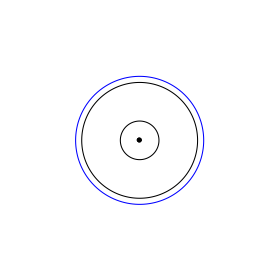
Abb. 1: Beispiele
5 Sonderfall Apolloniuskreis
Im Sonderfall r1 = r2 = 0 ergeben sich Apolloniuskreise und Mittelsenkrechte (Abb. 2).
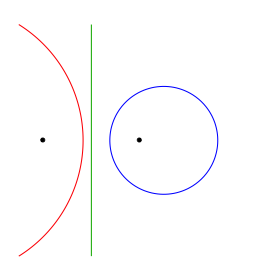
Abb. 2: Apolloniuskreise