Hans Walser, [20230316]

Bumerang

Idee und Anregung: B. B., B. und M. S., CH.

1 Problemstellung

Die implizite Gleichung

x^(2*n) + y^(2*n) - (x^n + y^n) - c = 0

hat für c := -1/5 und n := 7 die Darstellung der Abbildung 1.

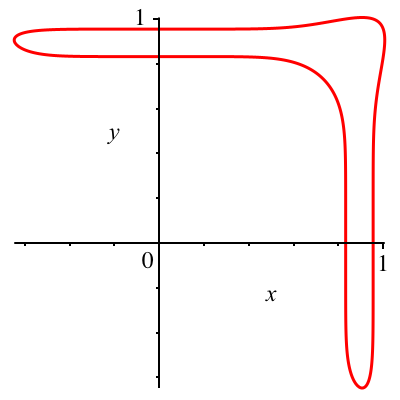
Abb. 1: Bumerang

Gesucht ist eine Polardarstellung der Kurve.

2 Bearbeitung

Der Ansatz

x := r*cos(phi), y := r*sin(phi)

ergibt für r zwei Lösungen:

r1 := ((cos(phi)^n + sin(phi)^n + sqrt(4*(cos(phi)^(2*n) + sin(phi)^(2*n))*c + (-cos(phi)^n - sin(phi)^n)^2))/(2*(cos(phi)^(2*n) + sin(phi)^(2*n))))^(1/n)

r2 := ((cos(phi)^n + sin(phi)^n - sqrt(4*(cos(phi)^(2*n) + sin(phi)^(2*n))*c + (-cos(phi)^n - sin(phi)^n)^2))/(2*(cos(phi)^(2*n) + sin(phi)^(2*n))))^(1/n)

In schönerer Schreibweise:

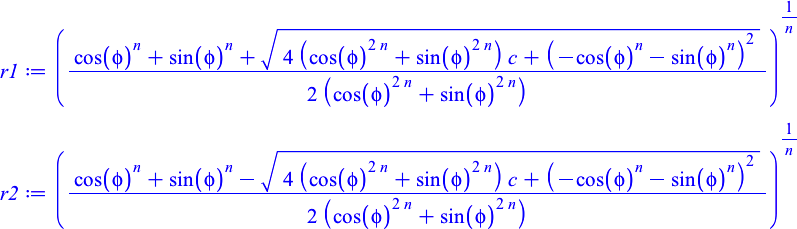
Die beiden Lösungen unterscheiden sich im Vorzeichen vor der Quadratwurzel. Der Grund für die beiden Lösungen ist das Auftreten einer quadratischen Gleichung.

Wir haben also nicht eine, sondern zwei Polardarstellungen:

x1 := r1*cos(phi), y1 := r1*sin(phi)

x2 := r2*cos(phi), y2 := r*sin(phi)

In der Abbildung 2 ist die erste Polardarstellung blau, die zweite grün gezeichnet.

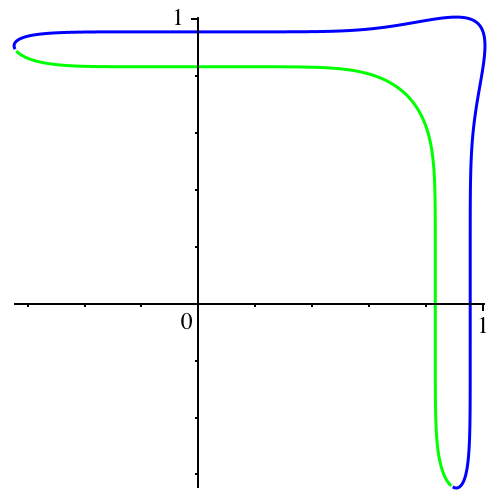
Abb. 2: Die beiden Lösungen

Die erste Lösung gibt vom Ursprung aus gesehen die Außenkontur, die zweite die Innenkontur.

3 Mittelweg

In der Abbildung 3 ist auch noch der Mittelweg eingezeichnet.

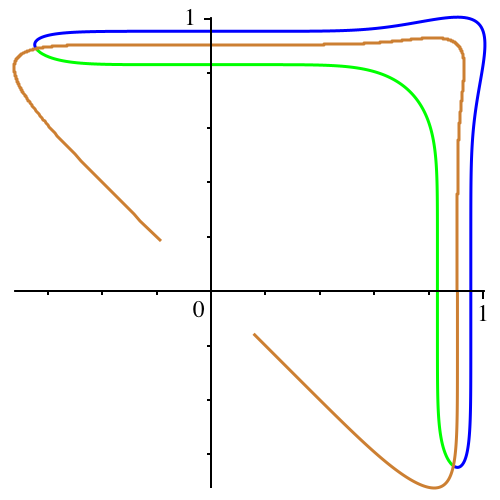
Abb. 3: Mittelweg

Er entsteht, indem beim Radius der Wurzelanteil weggelassen wird:

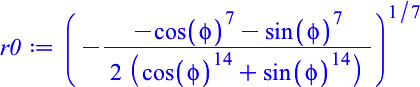
Dass der Mittelweg nicht genau in der Mitte liegt, hat mit dem Exponenten 1/n zu tun.

Der Parameter c kommt nur im Wurzelanteil vor. Der Mittelweg ist also unabhängig von c.

4 Nur eine einzige Polardarstellung

Um die Kurve mit einer einzigen Polardarstellung zu beschreiben, müsste das Zentrum ins Innere, zum Beispiel in den Punkt (0.9, 0.9) verlegt werden. Ich habe dies aber nicht durchgerechnet.

5 Variationen

In der Abbildung 4 variiert c von -0.5 (exklusive) bis 0 (inklusive). Hingegen bleibt n := 7 konstant. n ist ungerade. Die Figuren erinnern teilweise an Bumerangs.

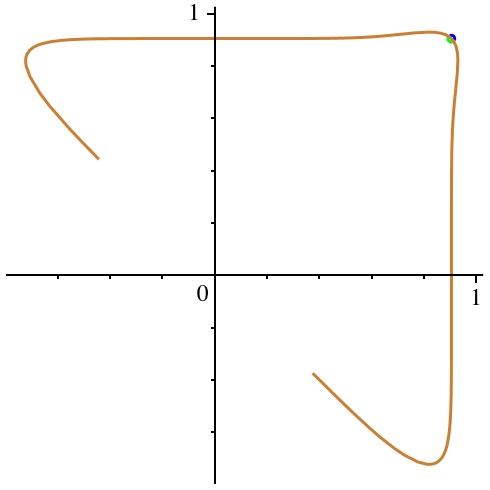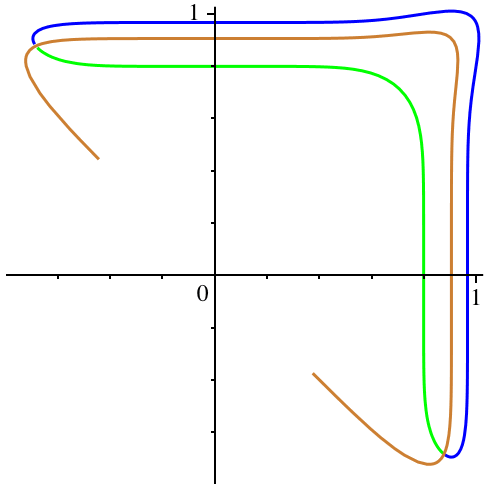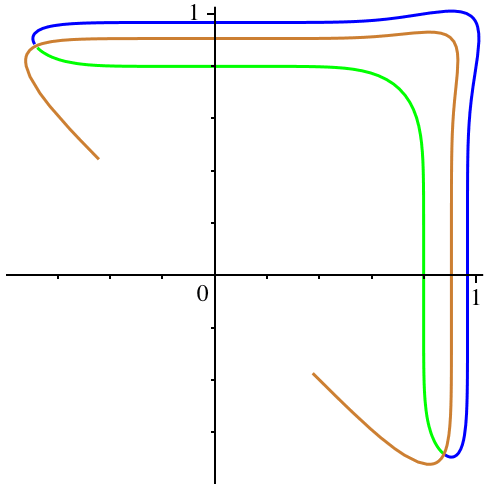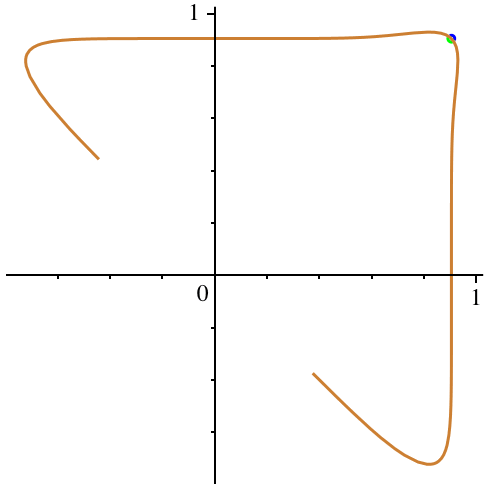
Abb. 4: Variation von c. n = 7

In der Abbildung 5 variiert c ebenfalls von -0.5 (exklusive) bis 0 (inklusive). Hingegen bleibt n := 6 konstant. Wir haben also ein gerades n. Die Figuren haben die Symmetrien des Quadrates. Keine Bumerangs.

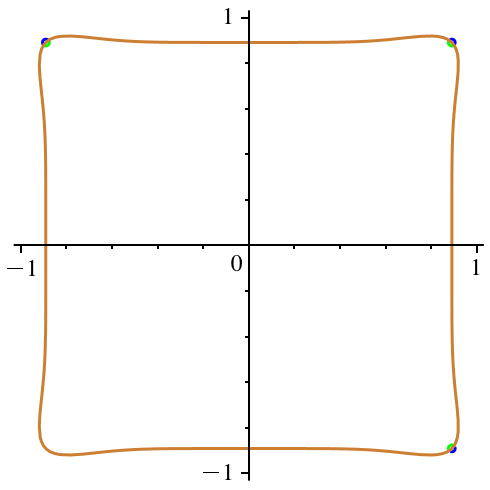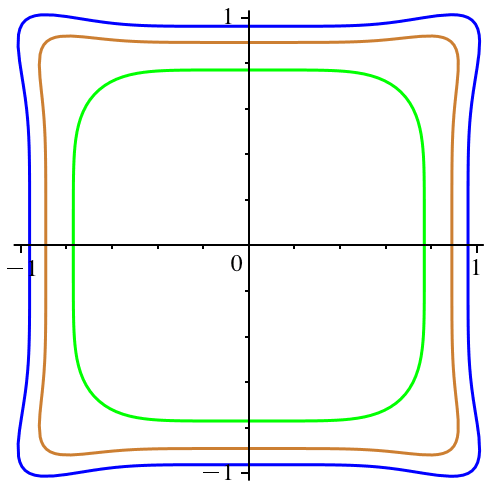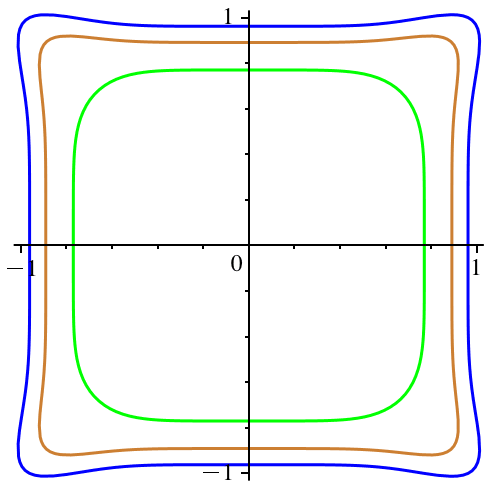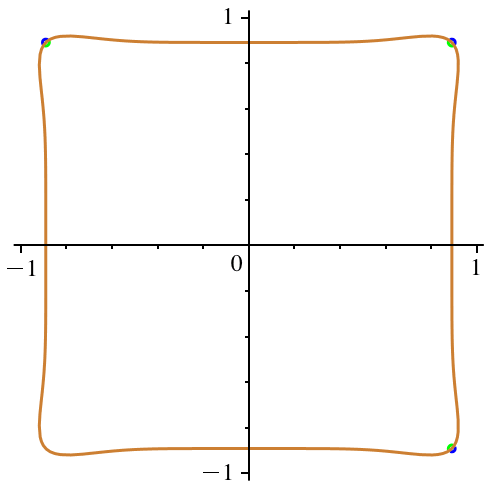
Abb. 6: Variation von c. n = 6

Bezüglich n haben wir einen Paritätsunterschied.

In der Abbildung 6 ist n ungerade und variiert von 1 bis 39. Kreis und Bumerangs.

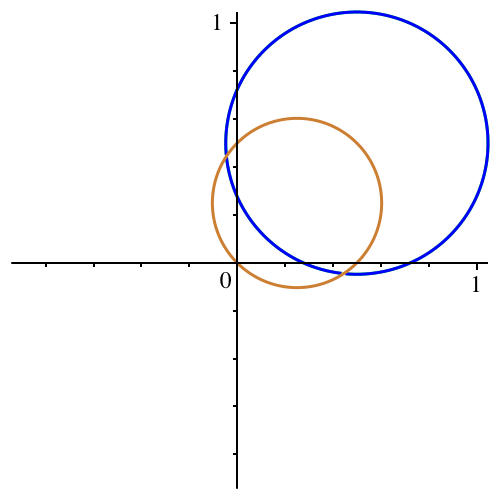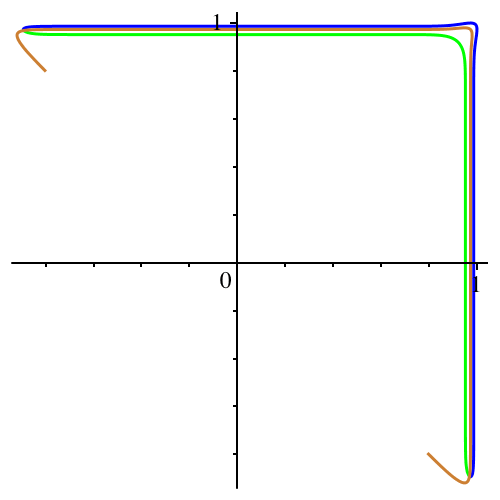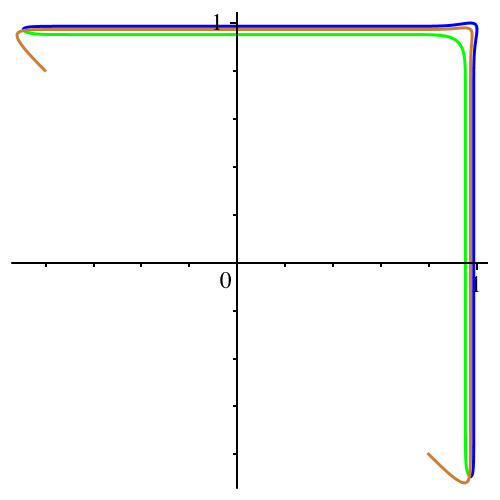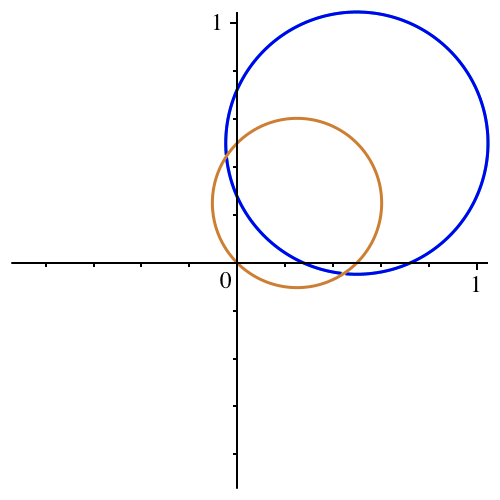
Abb. 6: Ungerades n

In der Abbildung 7 ist n gerade und variiert von 2 bis 40. Hingegen ist c := -1/5 konstant. Keine Bumerangs, sondern Figuren mit den Symmetrien des Quadrates.

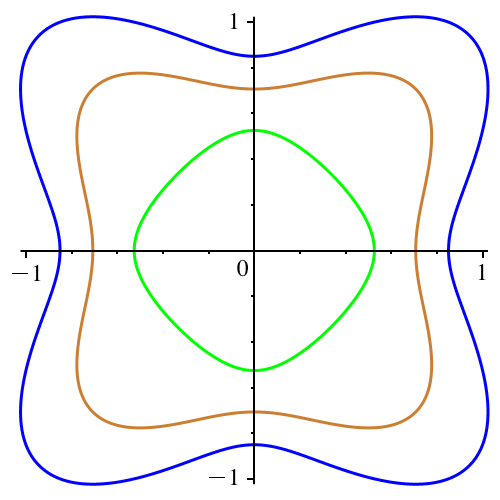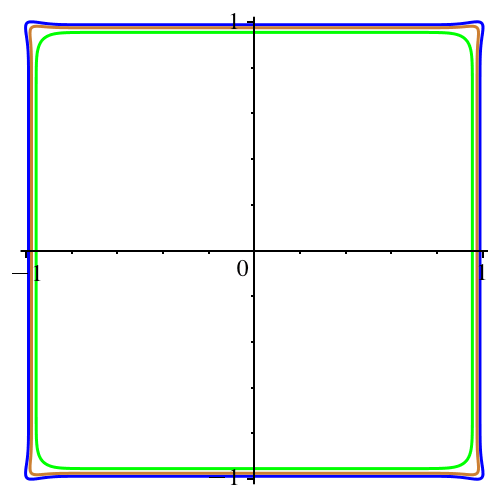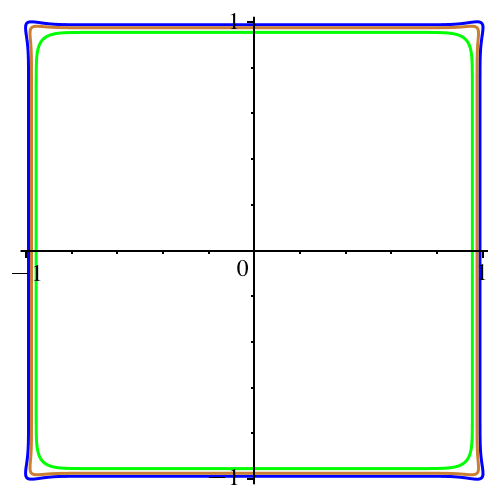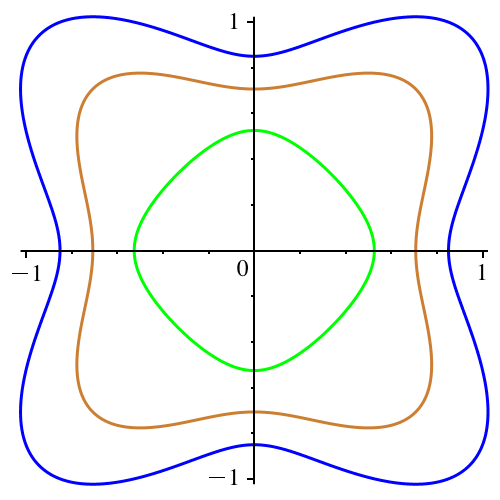
Abb. 7: Gerades n

6 Der Sonderfall und der Goldene Schnitt

Die Abbildung 8 zeigt die Kreise für den Sonderfall n := 1. Der grüne Kreis wird vom blauen zugedeckt, ist also bezüglich Größe und Lage mit diesem kongruent – Kongruenz im wörtlichen Sinne. Weiter sei c := -1/5.

Abb. 8: Sonderfall mit Kreisen. Goldener Schnitt

Der kleine Kreis hat den Mittelpunkt [1/4,1/4] und den Radius sqrt(2)/4.

Der blaue Kreis hat den Mittelpunkt [1/2,1/2] und den Radius sqrt(3/10). Nachweis durch Rechnung. Der Ursprung und die beiden Schnittpunkte mit der x-Achse sind im Verhältnis des Goldenen Schnittes. In der Abbildung 8 sind der Major rot und der Minor blau eingezeichnet.

Weblinks

Hans Walser: Bumerang und Affensattel

http://www.walser-h-m.ch/hans/Miniaturen/B/Bumerang/Bumerang.htm