Hans Walser, [20100612a]
Binomialkoeffizienten modulo eine Zahl
1
Worum geht es?
Die
Binomialkoeffizienten 
werden
einerseits wie Ÿblich mit einer festen Zahl moduliert, andererseits aber auch
mit den variablen Zahlen n und k. Entsprechend wird eingefŠrbt. Die Resultate hŠngen
mit dem kleinen Satz von Fermat zusammen.
2
Binomialkoeffizienten
Diese werden in einem
Hexagonalraster dargestellt.
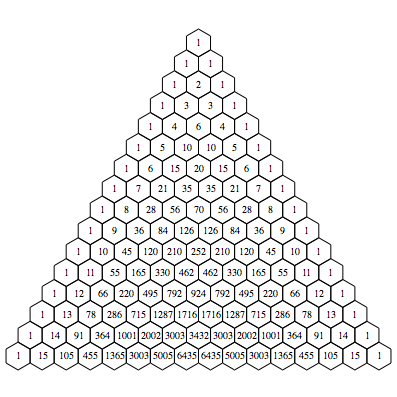
Binomialkoeffizienten
3
Binomialkoeffizienten modulo m
3.1
Modulo 2
Wir tragen jeweils 
ein. Wir
unterscheiden also die Binomialkoeffizienten nur bezŸglich gerade und ungerade.
Binomialkoeffizienten
modulo 2
3.2
Zwei Farben
Wir fŠrben nun die
Sechsecke mit zwei Farben ein. Wir erkennen die Struktur des Sierpinski-Dreieckes.
Bicolor
Dazu noch ein grš§erer
Ausschnitt.
Grš§erer Ausschnitt
Wir haben ein schšnes
schwarzes Dreieck in der Mitte.
3.3
Drei Farben
Wir tragen 
ein und fŠrben
entsprechend mit drei Farben.
Der Farbcode variiert
mit der Anzahl der Farben. Die Einsen auf dem Dach haben daher eine andere
Farbe. Die Zahl Null wird aber immer schwarz eingefŠrbt.
Den Ausschnitt wŠhlen
wir passend, sodass eine schšne Figur entsteht.
Modulo 3
Wir haben ein schwarzes
Dreieck in der Mitte.
3.4
Vier Farben
Modulo 4
Das schwarze Dreieck in
der Mitte ist nicht vollstŠndig schwarz.
3.5
FŸnf Farben
Modulo 5
In der Mitte ist ein
vollstŠndig schwarzes Dreieck.
3.6
Sechs Farben
Modulo 6
Die Figur ist etwas
eigenartig.
3.7
Sieben Farben
Modulo 7
Nun wieder ein vollstŠndig
schwarzes Dreieck in der Mitte.
3.8
Acht Farben
Modulo 8
3.9
Neun Farben
Modulo 9
3.10
Zehn Farben
Modulo 10
3.11
Primzahlen
Es fŠllt auf, dass wir
bei den Primzahlen jeweils Zeilen haben, die mit Ausnahme der beiden Enden
vollstŠndig schwarz sind, also der Zahl null entsprechen (in allen verwendeten
Farbcodierungen entspricht die schwarze Farbe der Zahl null). Diese schwarzen
Zeilen sind dann die Oberkante eines hŠngenden vollstŠndig schwarzen
gleichseitigen Dreieckes. Dies ergibt sich aus der Rekursion der
Binomialkoeffizienten. Zur Primzahl p
sind diese schwarzen Zeilen — soweit Ÿbersehbar — auf den Niveaus 
. . Beweis
folgt.
4
Binomialkoeffizienten modulo n
Wir tragen nun 
ein. Die
Modulzahl nimmt also pro Zeile um eins zu.
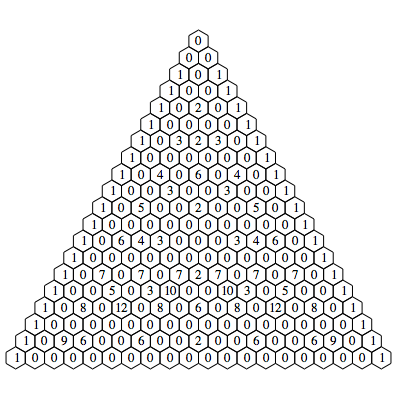
Modulo n
Bei den Zeilen mit
Primzahlniveau haben wir mit Ausnahme der Enden ausschlie§lich Nullen.
Nun fŠrben wir
entsprechend. Das gibt schwarze Zeilen bei den Primzahlniveaus.
Modulo n
5
Binomialkoeffizienten modulo k
Wir tragen nun 
ein und fŠrben
entsprechend.
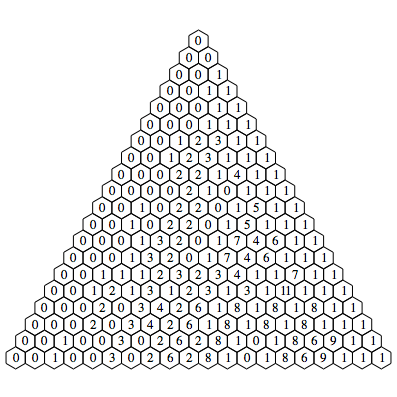
Modulo k
Farben modulo k
Sind Strukturen
erkennbar?
6
Zahlentheoretisches
Wir zeigen: FŸr eine
Primzahl p und 
gilt:
Es ist:
Wir mŸssen zeigen, dass
dieser Ausdruck mindestens einen Primfaktor p enthŠlt.
Wegen 
kšnnen die
Zahlen im Nenner einzeln hšchstens die einschlŠgige Primfaktorpotenz 
enthalten. Wenn
nun eine der Zahlen 
eine solche
Primfaktorpotenz 
mit 
enthŠlt, dann
ist dies auch fŸr die Zahl 
im ZŠhler der
Fall. Wir kšnnen diese Primfaktorpotenz also herauskŸrzen. Sollte k selber eine solche Primfaktorpotenz enthalten, so
kšnnen wir diese aus 
im ZŠhler herauskŸrzen,
und es bleibt im ZŠhler noch mindestens ein Primfaktor p Ÿbrig.
7
Der kleine Satz von Fermat
Der kleine Satz von
Fermat besagt: FŸr eine Primzahl p und
eine natŸrlich Zahl a gilt:
Beispiel: Es sei 
. Interessant sind nur die Zahlen 
. Tabelle:
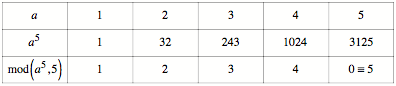
Der Beweis geht
induktiv Ÿber a. ZunŠchst ist 
.
Sei nun 
. Dann ist:
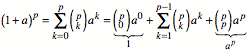
Wir haben oben gesehen,
dass fŸr eine Primzahl p und 
der
Binomialkoeffizient 
den Primfaktor p enthŠlt. Damit enthŠlt auch die Summe 
den Primfaktor p und es gilt:
