Hans Walser, [20210321]

Bananenkurve

Idee und Anregung: M. B., M.

1 Konstruktion mit Stab und Schnur

Wir bezeichnen den Nullpunkt eines kartesischen Koordinatensystems mit A (Abb. 1). Unterhalb von A ist der Punkt B höhenverstellbar auf der y-Achse festgemacht. In B ist ein Stab der Länge 1 gelenkig angemacht. Ebenfalls ist in B das eine Ende einer Schnur der Länge 1.2 befestigt. Diese Schnur wird durch eine Öse im Punkt A durchgeschlauft und dann mit dem anderen Ende am zweiten Ende C des Stabes befestigt.

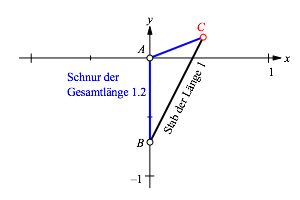
Abb. 1: Konstruktion

Geometrisch ist der Kreis um A mit der restlichen Schnurlänge als Radius zu schneiden mit dem Kreis um B mit dem Radius 1 (Abb. 2). Es gibt zwei zur y-Achse symmetrische Lösungen.

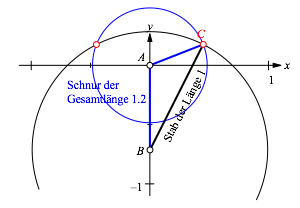
Abb. 2: Geometrische Konstruktion

Wenn wir nun den Punkt B etwas in die Höhe schieben (Abb. 3), wird das Teilstück BA der Schnur kürzer und das andere Teilstück AC entsprechend länger. Daher wird er Stab abgedreht.

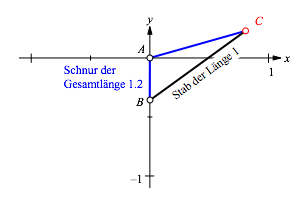
Abb. 3: Der Punkt B wird hinaufgeschoben

Die Abbildung 4 illustriert die Kinematik.

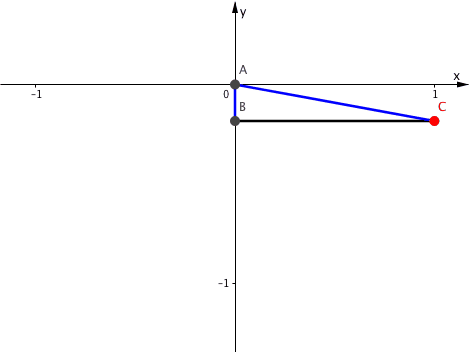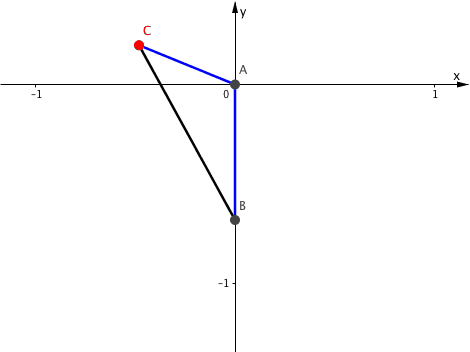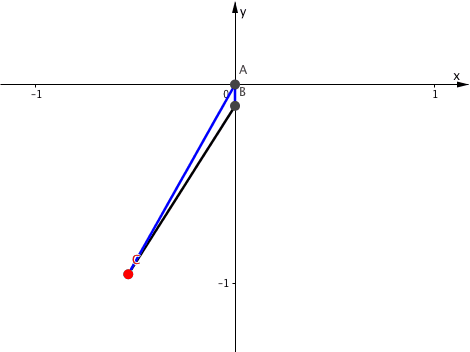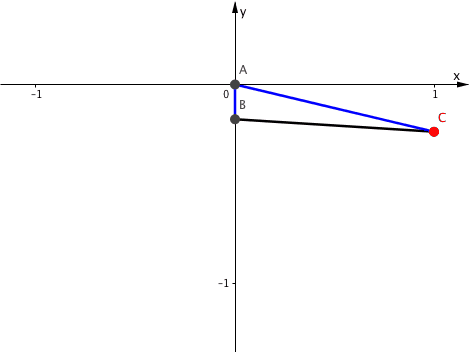
Abb. 4: Kinematik

2 Ellipse

Die Sache mit der Schnur konstanter Länge 1.2 erinnert an die Gärtnerkonstruktion (Abstandsdefinition) der Ellipse. Tatsächlich sind B und C die Brennpunkte einer Ellipse mit der Fadenlänge (Abstandssumme) 1.2. Die Ellipse verläuft in jeder Position von B durch den Punkt A (Abb. 5).

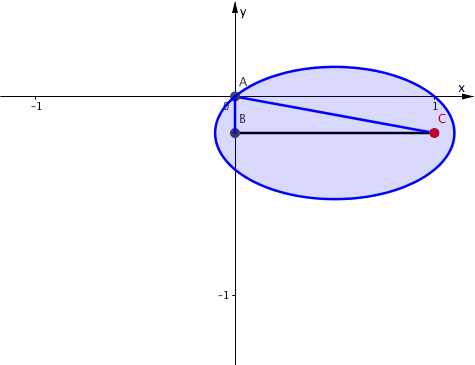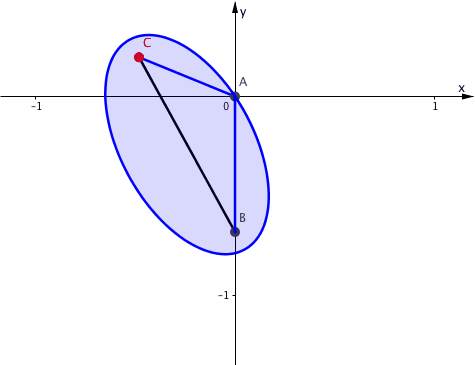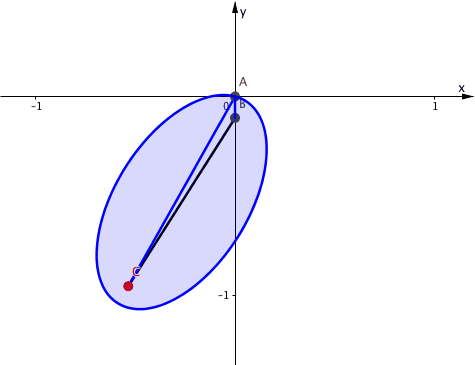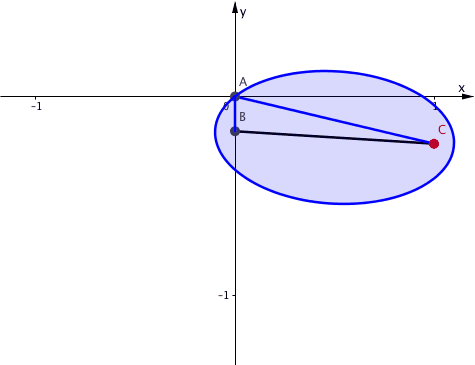
Abb. 5: Ellipse

3 Die Kurve

Wir fragen nach der Bahnkurve von C beim Hinauf- und Hinabschieben des Punktes B. Man kann das mit dynamischer Geometrie Software sehr einfach zeichnen. Die Abbildungen 6 und 7 zeigen die Bahnkurve zusammen mit den Konstruktionsbeispielen der Abbildungen 1 respektive 3. Die Form der Kurve erinnert an den Umriss einer Banane.

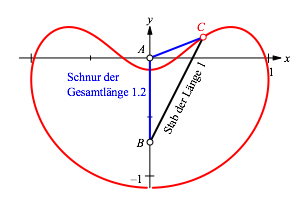
Abb. 6: Bahnkurve

Abb. 7: Bananenkurve

Die Abbildung 8 zeigt die Kinematik der Situation.

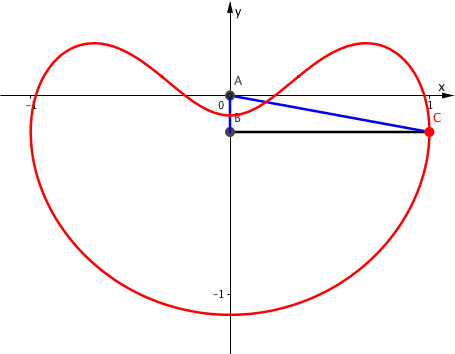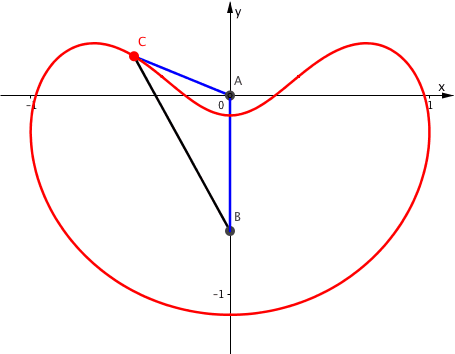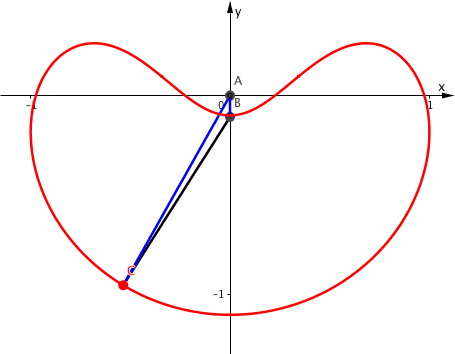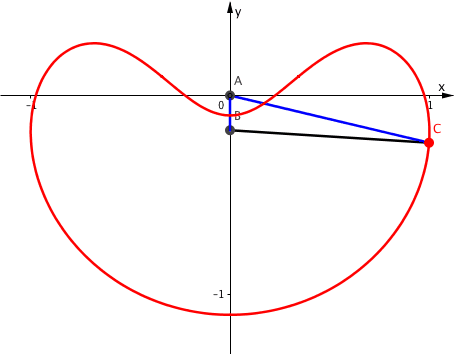
Abb. 8: Bahnkurve

In der Abbildung 9 ist zusätzliche die Ellipse angegeben.

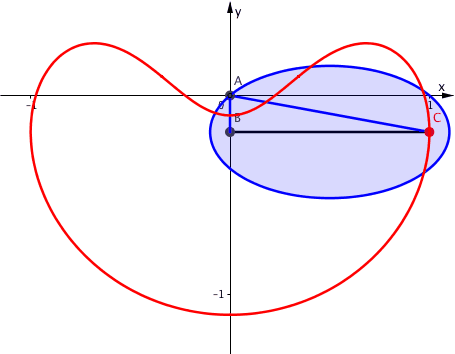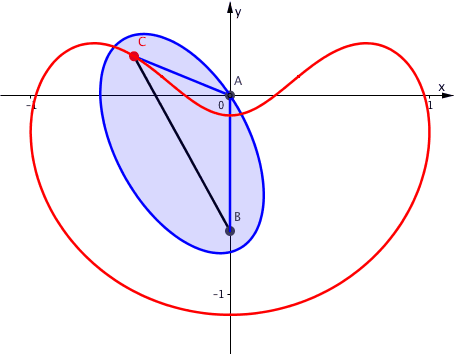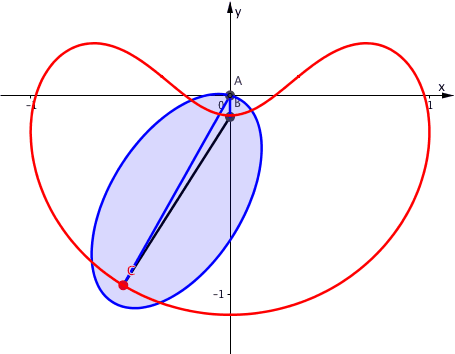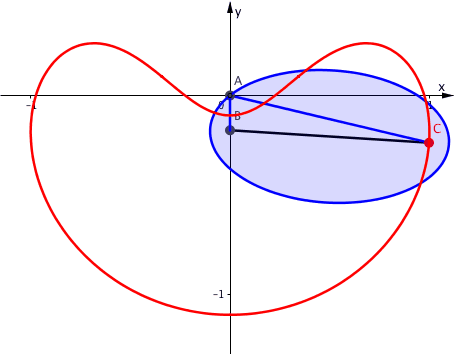
Abb. 9: Ellipse und Bahnkurve

4 Variation der Schnurlänge

Wir können die Schnurlänge zwischen 1 und unendlich variieren. In der Abbildung 10 variiert die Schnurlänge zwischen 1 und 3.

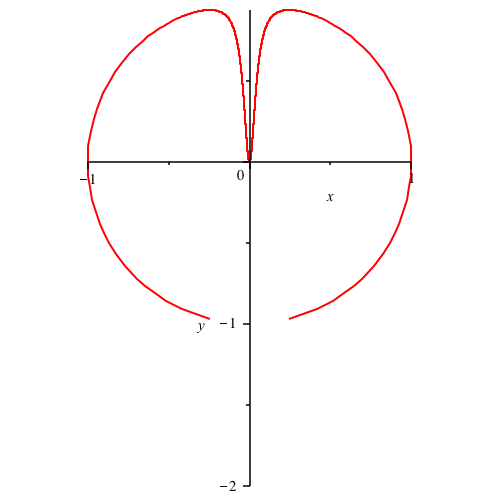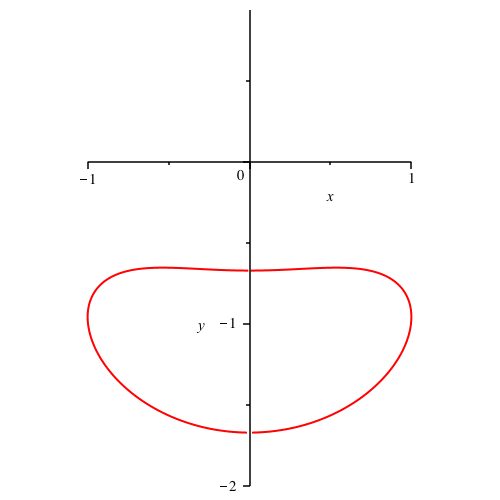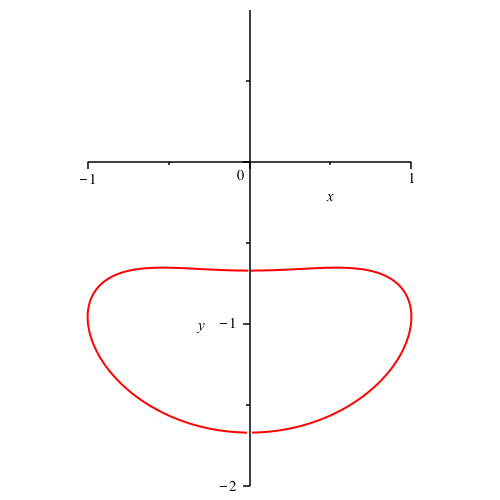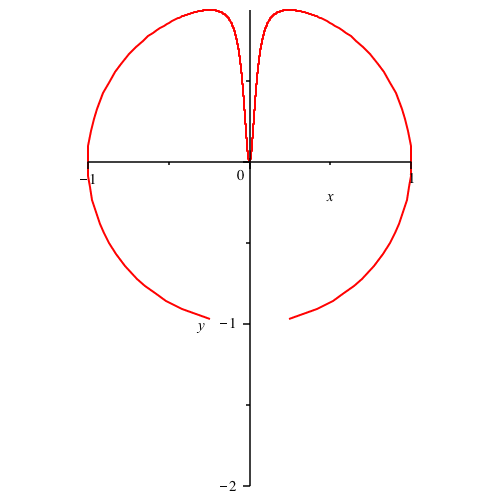
Abb. 10: Variation der Schnurlänge

5 Grenzfälle

Für die Schnurlänge 1 erhalten wir den von oben bis in die Mitte eingeschlitzte Einheitskreis (Abb. 11). Die Leserin oder der Leser ist eingeladen, sich die Kinematik dafür zu überlegen.

Abb. 11: Grenzfall Schnurlänge 1

Für den Grenzfall einer unendlich langen Schnur ergibt sich die Ellipse mit den Halbachsen 1 und 0.5 (Abb. 12). Der Mittelpunkt des Stabes verschiebt sich auf der langen Ellipsenachse.

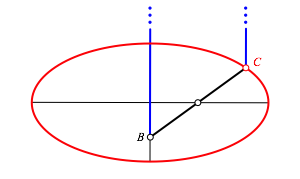
Abb. 12: Unendlich lange Schnur