Hans Walser, [20200114]
Aufwickel-Pythagoras
1 Worum geht es?
Kinematische Illustration des Satzes von Pythagoras mit archimedischen Spiralen. Der Focus wird dabei auf die Invarianz der Summe der Kathetenquadrate gelegt.
2 Motivation
Das Wesentliche des Satzes von Pythagoras ist die Invarianz der FlŠchensumme der Kathetenquadrate bei einer VerŠnderung der Ecke mit dem rechten Winkel auf dem Thaleskreis (Abb. 1).
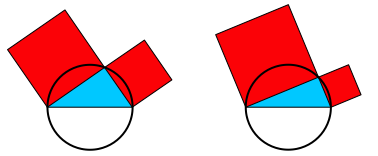
Abb. 1: Invariante FlŠchensumme der Kathetenquadrate
Im Grenzfall mit einer Kathete gegen null und der anderen gegen die Hypotenuse ergibt sich dann auch die FlŠchengleichheit mit dem Hypotenusenquadrat und damit die schulisch źbliche Formulierung des Satzes von Pythagoras.
Die Quadrate kšnnen durch irgendwelche zueinander Šhnliche Figuren ersetzt werden, insbesondere auch durch Kreise (Abb. 2).
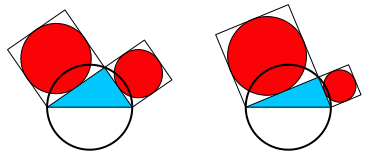
Abb. 2: Invariante KreisflŠchensumme
Die Abbildung 3 zeigt ein aufgewickeltes nicht mehr brauchbares Kletterseil.

Abb. 3: Kletterseil
Ein aufgewickeltes Seil ist im Prinzip eine archimedische Spirale. Wir werden die Kathetenquadrate durch archimedische Spiralen ersetzen.
3 Disposition
Das rechtwinklige Dreieck ABC mit dem rechten Winkel in C steht senkrecht auf der Hypotenuse c (Abb. 4).
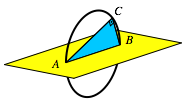
Abb. 4: Das rechtwinklige Dreieck
In den Katheten a und b setzen wir je eine Ebene rechtwinklig zur Dreiecksebene an. Diese beiden Ebenen bilden also ein in der Regel asymmetrisches Satteldach (Abb. 5).
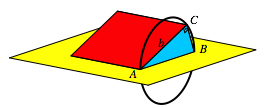
Abb. 5: Schiefes Satteldach
4 Spiralen
In diese Ebenen, die wir uns vergrš§ert denken, legen wir archimedische Spiralen mit den Zentren in A beziehungsweise B, welche bis zum Punkt C reichen (Abb. 6).

Abb. 6: Archimedische Spiralen
5 Auf- und Abwickeln
Die beiden Spiralen gehen an der Ecke mit dem rechten Winkel glatt ineinander źber, allerdings mit einer Torsion von 90ˇ. Wir kšnnen von einer Doppelspirale reden.
Wenn wir also die eine Spirale abwickeln und die andere um gleich viel aufwickeln, bleibt die von den Spiralen beanspruchte FlŠche insgesamt invariant. Wir sind also in der Situation des Satzes von Pythagoras.
Interessant ist dabei, dass wir sowohl eine FlŠcheninvarianz haben, wie beim Satz von Pythagoras źblich, wie auch eine LŠngeninvarianz. Die GesamtlŠnge der Doppelspirale bleibt invariant.
Die Abbildungssequenz 7 zeigt einige Stationen dieses Auf- und Abwickelprozesses.




Abb. 7: Auf- und Abwickeln
Die Animation 1 illustriert den Sachverhalt.

Animation 1: Ansicht
Die Animationen 2, 3 und 4 geben verschiedene Ansichten.

Animation 2: Sicht von oben

Animation 3: Sicht von vorne

Animation 4: Sicht von der Seite
Unsere Spiralen waren relativ dźnn, damit die rŠumliche Situation besser erfasst werden kann.
In den Animationen 5 bis 8 wurde die Dicke der Spiralen dem Kletterseil (Abb. 3) entsprechend gewŠhlt.

Animation 5: Ansicht

Animation 6: Sicht von oben

Animation 7: Sicht von vorne

Animation 8: Sicht von der Seite