Hans Walser, [20140818]

Anzahl Quadrate

Anregung: T. H. , A.

1 Worum geht es?

Gesucht ist die Anzahl der Quadrate, in ein quadratisches Gitter mit n×n Gitterpunkten eingezeichnet werden können. Die Quadratecken sollen Gitterpunkte sein. Ein Gitter mit n×n Gitterpunkten liegt in einem Quadrat der Seitenlänge n – 1.

Die Abbildung 1 zeigt ein Beispiel eines schrägen Quadrates in einem Gitter mit 6×6 Gitterpunkten.

Abb. 1: Quadrat im Gitter

2 Programm

Wir unterscheiden

A) Quadrate, deren Seiten parallel zu den Gitterlinien sind (bodenständig)

B) Quadrate, deren Diagonalen parallel zu den Gitterlinien sind

C) Allgemein schräge Quadrate

Nachfolgend ein Maple-Programm (für n = 6):

n:=6: # Groesse des n*n Gitters

# A:= Anzahl bodenstaendige Quadrate

A:=0:

for a from 1 to n-1 do

A:=A+a^2:

end:

print("A" =A);

# B:= Anzahl Quadrate mit Steigungswinkel 45°

B:=0:

for b from 1 to n do

if n-2*b > 0 then B:=B+(n-2*b)^2 end:

end:

print("B"=B);

# C:= Anzahl schraege Quadrate

C:=0:

for c from 2 to n-1 do

for d from 1 to c-1 do

if n-c-d > 0 then C:=C+(n-c-d)^2 end:

end:

end:

C:=2*C:

print("C"=C);

Total:=A+B+C

print("Total"=Total);

"A" = 55

"B" = 20

"C" = 30

"Total" = 105

3 Resultate

Die Tabelle 1 gibt die ersten Werte.

n	A	B	C
1	0	0	0	0
2	1	0	0	1
3	5	1	0	6
4	14	4	2	20
5	30	10	10	50
6	55	20	30	105
7	91	35	70	196
8	140	56	140	336
9	204	84	252	540
10	285	120	420	825

Tab. 1: Werte

3.1 Die A-Folge

Die A-Folge ist als Summe der Quadratzahlen eine arithmetische Folge 3. Ordnung.

Wenn wir Kugeln aufschichten gemäß Abbildung 2, ist die Gesamtzahl der Kugeln in einer Pyramide mit n Schichten die Zahl mit der Nummer n + 1 in der A-Folge.

Abb. 2: 140 Kugeln

3.2 Die B-Folge

Die B-Folge erscheint im Pascalschen Dreieck der Binomialkoeffizienten (Abb. 3).

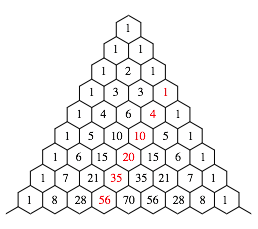
Abb. 3: Im Pascalschen Dreieck

Sie ist ebenfalls eine arithmetische Folge 3. Ordnung.

3.3 Die C-Folge

Für die C-Folge habe ich keine Illustration gefunden. Sie ist eine arithmetische Folge 4. Ordnung.

4 Die Formel

Wegen der C-Folge ist auch die Folge eine arithmetische Folge 4. Ordnung. Sie hat die recht einfache Formel:

Diese Formel ist vorerst nur empirisch erhärtet.

5 Beweis

Beweis mitgeteilt von T. H., A.

Der Beweis beruht darauf, dass jedes Quadrat in ein gitterparalleles Quadrat eingepackt werden kann (Abb. 4).

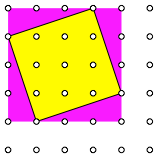
Abb. 4: Einpacken in gitterparalleles Quadrat

Zwischenbemerkung: In der Abbildung 4 haben wir die optische Täuschung, dass wir das gitterparallele Quadrat (magenta) schief zu sehen glauben.

Umgekehrt können in ein gitterparalleles Quadrat der Seitenlänge k genau k Quadrate einbeschrieben werden (Abb. 5 für k = 4). Dabei wird das gitterparallele Quadrat mitgezählt.

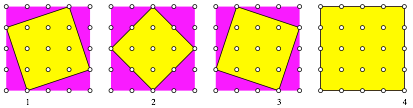
Abb. 5: Einbeschriebene Quadrate

Wir zählen zunächst die gitterparallelen Quadrate ab. In einem n×n Gitter gibt es gitterparallele Quadrate der Seitenlänge k. Dabei ist .

Zu jedem solchen gitterparallelen Quadrat gibt es k einbeschriebene Quadrate.

Somit ist:

Einsetzen der einschlägigen Formeln für die Summe der natürlichen Zahlen, der Quadratzahlen und der Kubikzahlen liefert:

6 Eine kleine Teilbarkeitsaufgabe

Zu zeigen: für jede natürliche Zahl n ist durch 12 teilbar.

Beweis mit Faktorisierung:

Es sind drei aufeinanderfolgende natürliche Zahlen als Faktoren im Spiel. Einer dieser Faktoren ist also durch 3 teilbar.

Und nun Fallunterscheideidung bezüglich der Parität von n:

· Bei geradem n hat mindestens zweimal den Primfaktor 2.

· Bei ungeradem n sind und gerade, wir haben also auch mindestens zwei Primfaktoren 2.

Damit ist der Ausdruck durch teilbar.