1 The problem

Find the indicated angle in Figure 1.

We will discuss a visual solution of this classical problem.

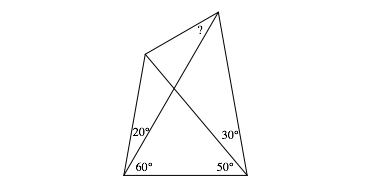
Fig. 1: Find the indicated angle

Of course we can draw the figure an will find 30°. But how can we prove it?

By the way: we have an angle of 20° in the figure. It’s not possible to construct an angle of 20° with ruler and compass only.

2 An isosceles triangle

The cyan triangle in fig. 2 is isosceles. In has the angles 80° and 50°. Hence the third angle is also 50°.

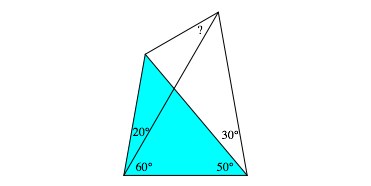
Fig. 2: Isosceles triangle

3 More isosceles triangles

First we introduce an equilateral triangle (red in figure 3).

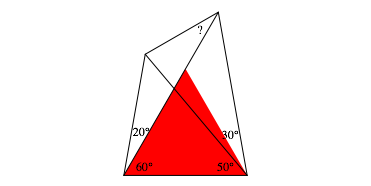
Fig. 3: An equilateral triangle

Because of the cyan isosceles triangle in figure 2 we find now another isosceles triangle (yellow in figure 4) beneath the red equilateral triangle. It has angles of 20° and twice 80°.

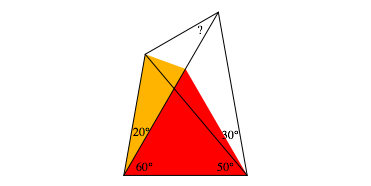
Fig. 4: Another isosceles triangle

Finally we can fit a congruent yellow isosceles triangle on the other side of the red equilateral triangle (fig. 5).

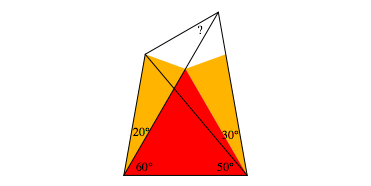
Fig. 5: A second yellow triangle

4 A star

The two yellow triangles in the position of figure 5 are part of a star (Fig. 6).

Fig. 6: The star

The star has a ninefold symmetry. In the center we have a regular nonagon.

5 A rectangle

Using two rhombuses (magenta in figure 7), a green equilateral triangle, and the symmetry of the star we find a rectangle (blue).

Fig. 7: A Rectangle

6 Right triangles

Hence the purple triangles in figure 8 are right triangles. Since one of the acute angles is 60°, the other must be 30°. This is the solution of our problem.

Fig. 8: Right triangles

7 Singular problem

We could solve our problem by help of a regular nonagon. This is due to the given angles. We cannot generalize the solution. Figure 9 gives a slightly modified problem that cannot be solved in this way.

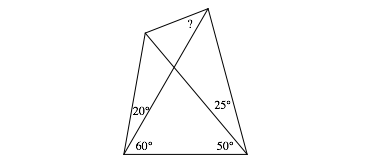
Fig. 9: Modified problem

The angle is about 38.73789306893789°.