Hans Walser, [20130727]

Dreieck und Sechseck

Anregung: H. K. S., L.

1        Worum geht es?

Es wird ein regelmŠ§iges Dreieck und ein dazu flŠchengleiches regelmŠ§iges Sechseck diskutiert. Dabei werden geometrische und rechnerische Methoden sowie Zerlegungsgleichheiten verwendet.

2        Im Quadratraster

Wir arbeiten in einem Quadratraster der Maschenweite 1 (Abb. 1).

 

Abb. 1: Quadratraster

 

Wir drehen nun Kopien dieses Rasters um 120¡ und 240¡ (Abb. 2).

 

Abb. 2: Verdrehte Raster

 

Wir erkennen Punkte, welche ein regelmŠ§iges Zwšlfeck bilden (Abb. 3).

 

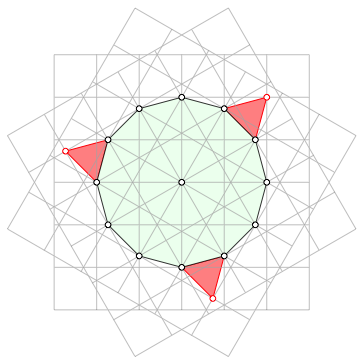
Abb. 3: Zwšlfeck

 

Wenn wir den Zwšlfeckseiten regelmŠ§ige Dreiecke aufsetzen, kommen deren Au§enecken auf Rasterunkte eines der drei Raster zu liegen.

3        Dreieck und Sechseck

Nun fŸhren wir ein regelmŠ§iges Dreieck (rot) und ein regelmŠ§iges Sechseck (blau) in die Figur ein gemŠ§ Abbildung 4.

 

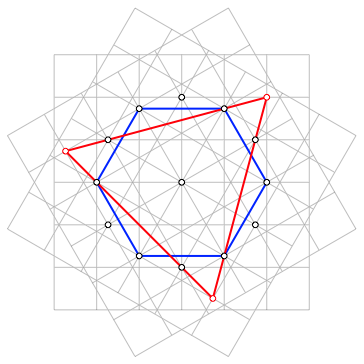
Abb. 4: Dreieck und Sechseck

 

Das rote Dreieck und das blaue Sechseck sind flŠchengleich.

Dies kann auf verschiedene Arten eingesehen werden.

4        FlŠchenverwandlungen

Wir kšnnen wir in der Schule mit FlŠchenverwandlungen arbeiten.

ZunŠchst haben das rote Dreieck  und das blaue Sechseck  das graue Dreieck  gemeinsam (Abb. 5).

 

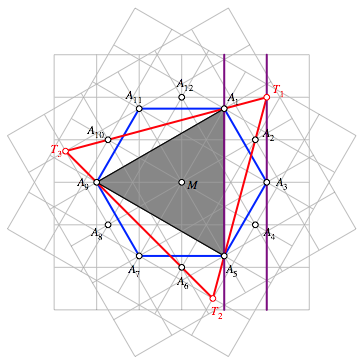
Abb. 5: FlŠchenverwandlungen

 

Aus der ParallelitŠt der beiden violetten Rasterlinien folgt die FlŠchengleichheit der beiden Dreiecke  und . Diese beiden Dreiecke haben eine gemeinsame Grundlinie  und die gleiche Hšhe 1 (Maschenweite des Rasters). Analog kšnnen wir an den anderen zwei Seiten des grauen Dreiecks Ÿberlegen.

5        Rechnerischer Nachweis

Das rote Dreieck hat den Umkreisradius  und damit den FlŠcheninhalt .

Das blaue Sechseck hat den Umkreisradius 2 und damit den gleichen FlŠcheninhalt .

6        Zerlegungsbeweis

Die Abbildung 6 zeigt das wesentliche Puzzle-Teil.

 

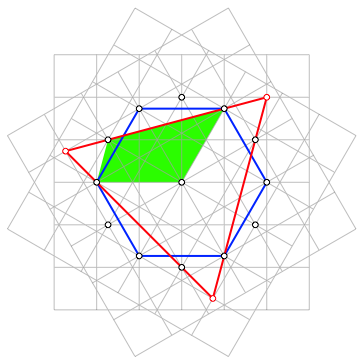
Abb. 6: Puzzle-Teil

 

Mit drei solcher Puzzle-Teilen (jeweils um 120¡ und 240¡ verdreht) kšnnen wir das rote Dreieck bis auf drei kleine Dreiecke an den Spitzen auffŸllen (Abb. 7).

 

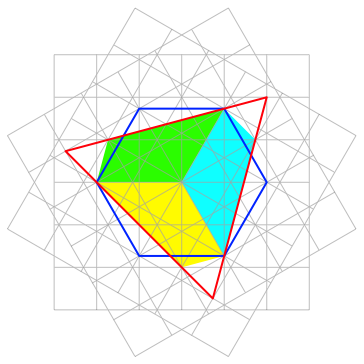
Abb. 7: Dreieck fast voll

 

Ebenso kšnnen wir damit das blaue Sechseck bis auf ein Dreieck im Zentrum auffŸllen (Abb. 8).

 

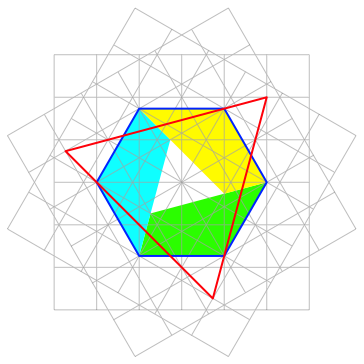
Abb. 8: Sechseck mit Loch

 

Als Restproblem mŸssen wir das Lochdreieck im blauen Sechseck auf die drei Eckdreiecke im roten Dreieck aufteilen. Wir haben das Problem der ãDreiecksdrittelungÒ. Die Abbildung 9 zeigt, wie das geht.

 

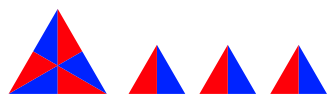
Abb. 9: Dreiecksdrittelung

 

Damit erhalten wir schlie§lich die gemeinsame Zerlegung des Dreiecks mit dem flŠchengleichen Sechseck (Abb. 10).

 

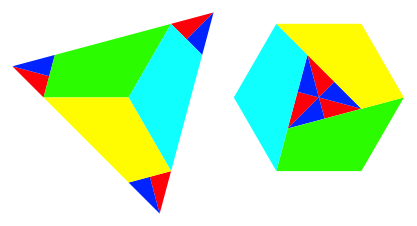
Abb. 10: Zerlegungsgleichheit