Jo Niemeyer, Hans Walser, [20070611a]
Goldener Schnitt
1 Konstruktion mit drei Rechtecken
Wir setzen drei beliebige kongruente Rechtecke zu einem Dreieck zusammen gemŠ§ Figur. Mit Hilfe eines Kreises kommen wir zum Goldenen Schnitt.
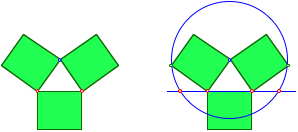
Drei kongruente Rechtecke
Es geht auch ãhochkantÒ.
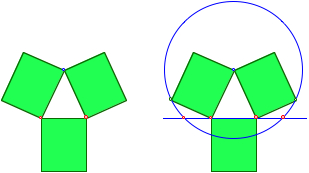
Hochkant
2 Beweis
Wir vereinfachen die Figur: Einem gleichschenkligen Dreieck setzen wir auf einem Schenkel ein Rechtreck auf, dessen andere Seite die BasislŠnge des Dreieckes hat. Der kreis um die Dreiecksspitze mit der Rechtecksdiagonalen als Radius fŸhrt zum Goldenen Schnitt.
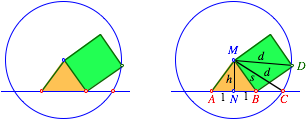
Vereinfachte Figur. Beweisfigur
Wir normieren die BasislŠnge des gleichschenkligen Dreieckes auf 2. Die Hšhe h ist variabel. Dann gilt:
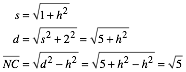
Wir sehen, dass die Hšhe h ãherausfŠlltÒ. Es ist dann:
Der Punkt B teilt also die Strecke AC im VerhŠltnis des Goldenen Schnittes.
3 SonderfŠlle
Diese Konstruktion enthŠlt als SonderfŠlle einige klassische Konstruktionen.
3.1 Halbes Quadrat
FŸr 
erhalten wir die
klassische Konstruktion, welche in einem Quadrat mit einer Seitenmitte
arbeitet. Das gleichschenklige Dreieck ist zu einer Strecke mit Mittelpunkt
degeneriert.
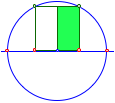
Halbes Quadrat
3.2 George Odom
FŸr 
ergibt sich die
Konstruktion von George Odom im gleichseitigen Dreieck (kopfstehend).
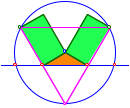
Figur von George Odom
Die Situation lŠsst sich auch in ein regelmŠ§iges Sechseck einbetten.
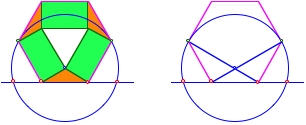
Sechseck. Minimalkonstruktion
3.3 Halbes Quadrat und Rechteck im DIN-Format
Hier ist 
.
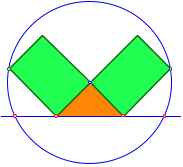
Halbes Quadrat und DIN-Rechtecke
Das passt in ein regelmŠ§iges Achteck.
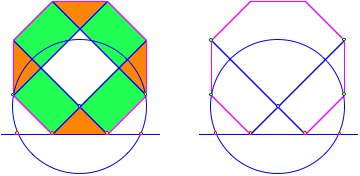
Achteck. Minimalkonstruktion
3.4 Gleichseitiges Dreieck und Quadrat
FŸr 
erhalten wir die
Figur mit einem gleichseitigen Dreieck und einem Quadrat.
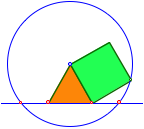
Gleichseitiges Dreieck und Quadrat
Die Figur passt in ein regelmŠ§iges Zwšlfeck.
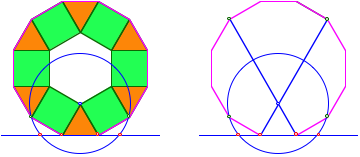
Zwšlfeck. Minimalkonstruktion